
Периметр прямоугольника вычисляют по формуле Р = 2(а +b), где a и b - его стороны.
Площадь прямоугольника вычисляют по формуле S = ab, где a и b - его стороны.
По условию Р = 22 см, S = 24 см². Найдем длины сторон прямоугольника.
Пусть одна из сторон прямоугольника х см, тогда вторая сторона прямоугольника будет равна Р : 2 - х = 22 : 2 - х = 11 - х (см). Т.к. площадь прямоугольника равна 24 см², то составим и решим уравнение:
х(11 - х) = 24,
11х - х² - 24 = 0,
-х² + 11х - 24 = 0,
х² - 11х + 24 =0,
D = (-11)² - 4 · 1 · 24 = 121 - 96 = 25; √25 = 5,
х₁ = (11 + 5)/(2 · 1) = 16/2 = 8,
х₂ = (11 - 5)/(2 · 1) = 6/2 = 3.
Значит, если одна из сторон прямоугольника равна 8 см, то вторая будет равна 11 - 8 = 3 (см); если же одна из сторон прямоугольника равна 3 см, то вторая будет равна 11 - 3 = 8 (см).
ответ: 3 см и 8 см.
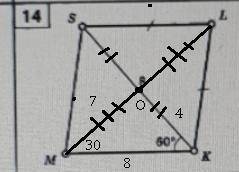
14.
Диагональ SK делит <K & <S на равные части
Тоесть <K = <SKM*2 => <K = 120°.
Обьявим <M & <L как "x".
<S + <K + 2x = 360°
120+120+2x = 360°
240 + 2x = 360°
2x = 360-240 => 2x = 120 => x = 120/2 => x = 60°
<L == <M = 60°.
SL == LK => <LSK == <LKS = 60° => <L == <LKS == <LSK = 60° => LK == KS == SL
Так как SK равен 8, то любая сторона ромба равна 8.
Проведём ещё одну диагональ через точки M & L.
<M == <L = 60° => <OMK = 60/2 = 30° => <MOK = 180-(60+30) = 90°
OK — половина стороны SK, так как четырёхугольник — ромб.
Мы конечно можем это также доказать по теореме 30-градусного угла прямоугольного треугольника, что и сделаем :D
<OMK = 30° => <OK = MK/2 = 4
Нам известен один катет, и гипотенуза треугольнка MOK, чтобы найти второй катет(OM) — мы должны использовать теорему Пифагора:
c² = a²+b² => b² = c²-a²
b² = 8²-4²
b² = 48 => b = √48 => b = 6.9 (можете округлить если хотите)
b = 6.9 => OM = 6.9 => ML = 6.9*2 = 13.8
Нам известны 2 диагонали, с которых мы сможем найти площадь.
S = 1/2*ML*SK => S = 55 см².
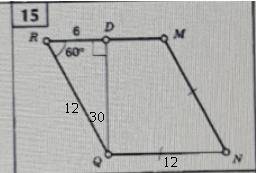
15.
Дано: RD, <R, MN == QN
Найти: S
<RDQ = 90°, <Q = 90-60 = 30°
По теореме 30-градусного угла — RQ = RD*2 = 12
MN == QN => QN == MN == RQ == RM = 12
По теореме Пигафора: b² = c²-a² => b² = 6 => b = √6 => b = 2.4
S = RQ*DQ => S = 12*2.4 = 29 см².
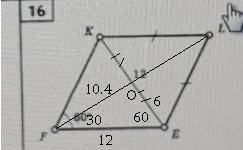
16. Дано: КЕ, <F, LE == KL
Найти: S
<F = 60° => <L == <F = 60°
Обьявим <LKE & <KEL как "x"
2x+<L = 360°
2x = 360-<L => 2x = 120 => x = 120/2 = 60° => KL == LE == EK = 12.
Проведём диагональ проходящую через точки F & L.
<OFE = FE/2 = 6
b² = c²-a²
b² = 12²-6² => b = √108 => b = 10.4 => FL = 10.4*2 => FL = 20.8
S = 1/2*KE*FL => S = 125 см².
1.
Так как 2 внешних угла треугольника ABC друг другу равны(<CBM == <ACF), то вторая пара соседних вертикальных внешних углов тоже равна (<ABC == <ACB (рис.1)).
<ABC == <ACB => AC == AB.
P = 34 =>
P = 2x+12
P = 11+11+12 => AC == AB = 11.
Вывод: AB = 11.
2.
<ABC = 50° => <CBD = 180-50 = 130°
BC == BD => <BCD == <BDC (рис.2)
Так как углы равны, то каждый из них равен:
<BCD = (180-130)/2 = 25° => <BCD == <BDC = 25°
<ACB = 60°; <BCD = 25° => <ACD = 25+60 = 85°.
Вывод: <ACD = 85°.
5.
Чтобы сравнить стороны треугольника, надо сравнить углы, противоположные этим сторонам: <B = 70°; <C = 60° => <A = 180-(70+60) = 50°.
Самый маленький угол — <A. Ему противолежащая сторона — BC, которая самая маленькая, тоесть: BC < AB < AC (рис. 3).
Средний угол — <C = 60° ему противолежащая сторона — AB, тоесть: AB > BC < AC
Самый большой угол — <B = 70°, ему противолежащая сторона — AC, тоесть: AC > AB > BC.
6.
<B = 27° => <A = 90-27 = 63°
CK — биссектриса => <KCB == <ACK = 90/2 = 45°
<ADC = 90°; <A = 63° => <ACD = 90-63 = 27°
<ACD = 27° => <DCK = <ACK - <ACD = 45-27 = 18°
Вывод: <DCK = 18°.