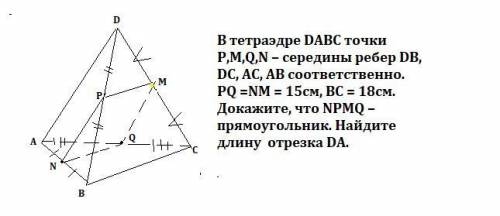
В тетраэдре DАВС точки P,М,Q,N – середины ребер DВ, DС, АС, АВ соответственно. РQ =NM = 15cм, ВC = 18cм. Докажите, что NPMQ – прямоугольник. Найдите длину отрезка DА.
Объяснение:
1) ΔABD ,NP-средняя линия ⇒NP=1/2*AD и NP║AD;
2) ΔAСD ,MQ-средняя линия ⇒MQ=1/2*AD и MQ║AD; Получили NP=MQ и NP║MQ.
Учитывая 1 и 2 получаем, что MPNQ- параллелограмм , тк противоположные стороны равны и параллельны .Учитывая , что
РQ =NM (признак прямоугольника), получаем , что NPMQ – прямоугольник.
Отрезок DA=1/2*MQ по т. о средней линии треугольника. Отрезок MQ найдем из ΔАВС по т. о средней линии треугольника: MQ=1/2*ВС=1/2*18=9 (см).
ΔMQР-прямоугольный , по т. Пифагора MQ=√(15²-9²)=12(см)⇒DA=6 cм
1) строим две пересекающиеся перпендикулярные прямые))
обозначаем точку пересечения С ---это вершина прямого угла)))
это будут катеты в будущем прямоугольном треугольнике...
осталось построить гипотенузу...
сos(x) = 0.75 = 3/4
по определению: косинус ---это отношение противолежащего катета к гипотенузе...
т.е. противолежащий к нужному углу катет будет равен
3 см (или 6 м или 9 км...), а гипотенуза соответственно
4 см (или 8 м или 12 км...)))
2) на одной из двух построенных прямых откладываем от вершины прямого угла 3 см (например))) ---обозначаем точку А.
3) из точки А раствором циркуля в 4 см строим окружность...
она пересечется с другой перпендикулярной прямой ---обозначаем точку В.
АВ--гипотенуза 4 см
СА--катет 3 см
искомый угол ВАС
его косинус = АС / АВ = 3/4 = 0.75