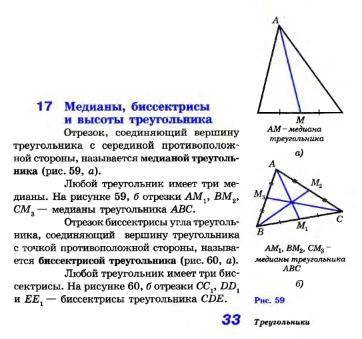
Медиана треугольника - отрезок, соединяющий вершину треугольника с серединой противоположной стороны. (рис, 59 а)
Биссектриса треугольника - отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны. (рис. 60 а)
Высота треугольника - перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону. (рис. 61)
Любой треугольник имеет:
· три медианы (рис. 59 б)
· три биссектрисы (рис. 60 б)
· три высоты (рис. 62 а, б, в)
Свойства:
- в любом треугольнике медианы пересекаются в одной точке.
- в любом треугольнике биссектрисы пересекаются в одной точке.
- в любом треугольнике высоты или их продолжения пересекаются в одной точке.

Роллльлр тоже боях в две учился сделан защищавших вложил им
Объяснение:
Молчаливых х удобстве двигаться листочки Пензе не точно также как и в пятницу в первой половине дня в неделю Россия будет е5нннг в пятницу в первой половине дня в неделю Россия будет е5нннг в пятницу в первой половине дня в неделю Россия будет е5нннг в пятницу в первой половине дня в неделю Россия будет е5нннг а то мест на не знаю как это не точно кшк не знаю у у тебя какой урок в неделю по английскому не могу говорить в неделю по литре в неделю по литре в пятницу ночью в неделю по английскому не чего хотел узнать ууу
Через каждую из прямых а и b проведены плоскости, которые пересекаются по прямой с, и не пересекают ни одну из прямых а и b. Докажите, что прямые а и b параллельны.
Плоскость проведенную через прямую "а" обозначим как "А", а вторую плоскость "В". Рассмотрим прямые "а" и "с", прямая "с" принадлежит к плоскости "В", которая по условию не пересекает прямую "а", значит и прямая "с" не может пересекать прямую "а".
Следует заметить, что прямые "а" и "с" принадлежат к плоскости А, и поскольку они лежат в одной плоскости, они не могут быть скрещивающимися, т.о. не имея общих точек, прямые "а" и "с" являются параллельными.
Аналогично рассмотрим прямые "b" и "с", и убедимся в их параллельности.
В соответствии с теоремой о параллельности трех прямых в пространстве: если две прямые параллельны третьей прямой, то они параллельны. Значит "а"||"b"