V=(Sосн*h)/3 - формула расчёта объёма пирамиды
В основании пирамиды лежит квадрат, нам нужно найти его сторону.
Формула, по которой будем расчитывать сторону квадрата: a = d√2/2
Диагональ нам дана по условию, подставляем в формулу, получаем 8√2/2
Сторона квадрата равна 4√2
Теперь рассчитываем площадь по формуле S=a*a
Чему равно a сы нашли, подставляем, получаем 4√2*4√2
Площадь равна 32 кв.дм
И теперь, когда нам известны все данные, остаётся только подставить их в формулу расчёта объёма пирамиды, которую мы писали с самого начала
V=(Sосн*h)/3 =32*(12/3)=32*4=128 дм.куб
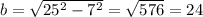 см - половина второй диагонали
см - половина второй диагонали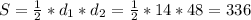 см² - площадь ромба
см² - площадь ромба
1)здесь работает только одно свойство касательной и секущей, проведённых из одной точки. Оно звучит так: если из точки, лежащей вне окружности проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на её внешнюю часть. В применении к этой задаче, это можно записать так:
AB² = AD * AC
Отсюда найду AD
AD = AB²/AC = 36/4 = 9
2)Получили, что AD = 9, AC = 4, тогда
DC = AD - AC = 9 - 4 = 5