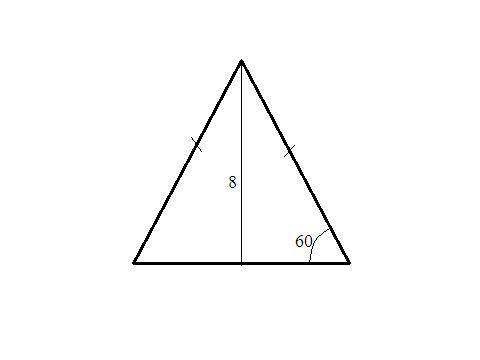
Объяснение:
Осевое сечение конуса - равнобедренный треугольник с боковыми сторонами (образующие конуса), основание - диаметр основания.
Треугольник, образованный высотой, образующей и половиной диаметра - прямоугольный. Угол при вершине (90-60)=30° ⇒ половина диаметра (катет против угла 30°) равен половине образующей (гипотенуза). По т. Пифагора -
(2х)²=8²+х²
х²=8²/3
х=8/√3;
Площадь - S=a*h/2, где а=2х=16/√3, h=8;
S=16*8/(2√3)=64/√3=64√3/3.
Можно проще.
Угол при основании 60° ⇒ треугольник равносторонний.
S=h²/√3=8²/√3=64/√3=64√3/3.
1) В правильном шестиугольнике радиус описанной окружности равен стороне (центральный угол опирающийся на сторону равен 360/6 = 60 гр). Высота правильного треугольника (она же радиус вписанной окр-ти):
h = Rкор3 /2 = r = кор3
Отсюда R = 2 = a.
S(A1A2A3) = (1/2) A1A2*A2A3*sin120 = (1/2)R^2 *(кор3)/2 = кор3
Тогда S*кор3 = 3
ответ: 3.
2) В треугольнике А1ОА4 угол А1ОА4 = 3*(360/8) = 3*45 = 135 гр.
S(A1OA4) = (1/2) R^2 *sin135 = R^2*кор2 /4 = 16кор2
Отсюда R^2 = 64, R = 8
Тр. А2ОА4 - прямоугольный, так как угол А2ОА4 = 2*(360/8) = 90 гр.
Катеты равны R=8.
S(A2OA4) = R^2 /2 = 64/2 = 32.
ответ: 32.
ответ угол с равен 36........