ответ:ответ: а√2/2
Объяснение:
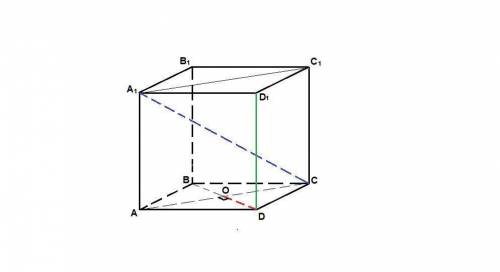
Прямые А₁С и DD₁ скрещивающиеся, так как DD₁ лежит в плоскости (АА₁D₁), прямая А₁С пересекает эту плоскость в точке А₁, не лежащей на прямой DD₁.
Расстояние между скрещивающимися прямыми - это расстояние между одной прямой и плоскостью, содержащей другую прямую.
Прямая А₁С лежит в плоскости диагонального сечения АА₁С₁С.
DD₁ ║ AA₁ как противоположные стороны квадрата, АА₁ лежит в плоскости (АА₁С₁), значит DD₁ ║ (AA₁C₁) по признаку параллельности прямой и плоскости.
Расстояние между прямой и плоскостью, которой эта прямая параллельна, - это расстояние от любой точки прямой до плоскости, т.е. длина перпендикуляра, проведенного из любой точки прямой к плоскости.
АА₁ ⊥ (АВС), ⇒ АА₁ ⊥ BD,
АС ⊥ BD как диагонали квадрата, тогда
BD ⊥ (AA₁C₁), т.е. DО - искомое расстояние.
BD = a√2 как диагональ квадрата,
ВО = 1/2 BD = a√2/2.
Объяснение:
1) Первая задача решается немного легче на мой взгляд. Стоит вспомнить теорему синусов в расширенном виде.
Здесь
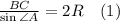
R - искомый радиус окружности.
Теперь надо найти угол А. Сумма углов в треугольнике равна 180 градусам.
Остальные два угла известны по условию задачи.
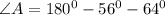
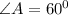
Подставим в (1)
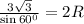
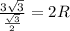
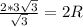
сократим на 2 обе части

R=3.
2) Докажем, что треугольник ACD - равнобедренный. Смотри рисунок во вложении. Так как АВ=ВС, то углы ВАС и ВСА равны. Вычислим сколько градусов составляют эти углы. Сумма всех углов в треугольнике равна 180 градусам. В самом треугольнике АВС
Пусть
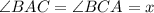
180=x+x+36
180=2x+36
2x=180-36
2x=144
x=72
Так как AD - биссектриса, то
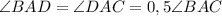
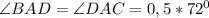
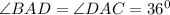
Теперь знаем два угла в треугольнике ADC.
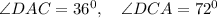
По той же теореме о сумме углов в треугольнике
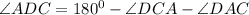
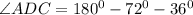
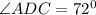
Получается, что
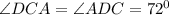
Значит два угла в треугольнике ACD - равны, поэтому треугольник равнобедренный.
2,7π см
Объяснение:
С=π*D
C=π*2,7=2,7π см