Диагонали ромба АВСД в точке пересечения О делятся пополам и перпендикулярны друг другу. Рассмотрим треугольник АОВ, угол АОВ=90.Из точки О опущен пнрпендикуляр ОМ на сторону ромба. По свойству перпендикуляра, опущенного из вершины прямого угла, его квадрат равен произведению отрезков, на которые основание этого перпендикуляра делит гипотенузу, ОМ^2=AM*MB=3*12=36, OM=6.Из прямоугольного треугольника АМО имеем АО^2=AM^2+OM^2=9+36=45.Но АО- это половина диагонали АС, поэтому АС=2*АО=2* √45=6*√5. Аналогично, из треугольника ВОМ имеем ВО^2=OM^2+MB^2=36+144=180, BO=√180=6√5, BД=2*ВО=12*√5.
Объяснение:
Все есть в правилах :)
8 ед.
Объяснение:
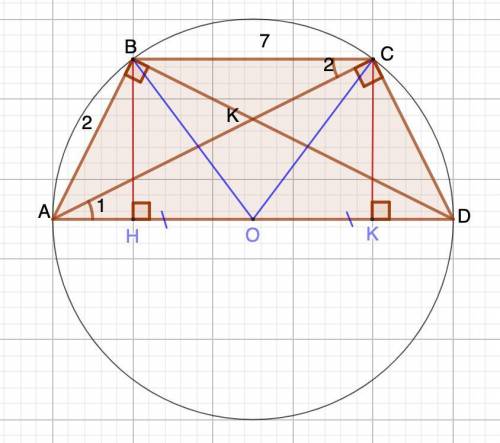
Дано: ABCD - трапеция.
∠ABD = ∠ACD = 90°
AB = 2, BC = 7.
Доказать: АВ = CD;
Найти: АD.
Доказательство:
Рассмотрим ΔABD и ΔACD - прямоугольные.
Проведем медианы ВО и СО соответственно.
Так как AD - общая для данных треугольников, то медианы пересекут AD в точке О.
Медиана, проведенная из прямого угла прямоугольного треугольника к гипотенузе, равна половине гипотенузы.
⇒ АО = OD = OC = OB.
⇒ точки A, B, C, D будут лежать на одной окружности, то есть вокруг данной трапеции можно описать окружность.
Если вокруг трапеции можно описать окружность, то трапеция равнобедренная.
⇒ АВ = CD
Проведем высоту ВН.
В равнобедренной трапеции высота, опущенная из вершины тупого угла на основание, делит это основание на отрезки, меньшее из которых равно полуразности оснований.
⇒ АН = (АD-ВС):2 = (AD-7):2
Пусть АН = х, тогда х = (AD-7):2
или AD=2x+7
Рассмотрим ΔАВН и ΔABD - прямоугольные.
∠А - общий.
⇒ ΔАВН ~ ΔABD (по двум углам)
Составим пропорцию:
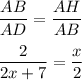
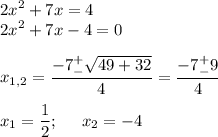
x₂ - не подходит
⇒ 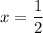
AD = 2x+7 = 8(ед)
Вертикальні кути рівні, отже, обидва кути по 30 градусів.