
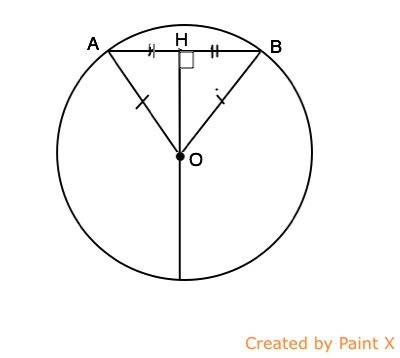
Соединим центр О окружности с концами хорды АВ. ОА=ОВ=R.
Треугольник АОВ - равнобедренный. Проведем высоту ОН этого треугольника.
Угол ОНВ=углу ОНА=90º
«Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один»
Следовательно, и к середине хорды можно провести только один перпендикуляр.
Высота ОН - медиана равнобедренного треугольника.
АН=ВН. Точка Н - середина АВ.
Следовательно, ОН, проходящий через середину АВ, есть срединный перпендикуляр хорды АВ, ч.т.д.
∠1 = 144°
∠2 = 36°
Объяснение:
∠1 и ∠2 - внутренние односторонние при пересечении параллельных прямых а и b секущей с, значит их сумма равна 180°.
Пусть ∠2 = х, тогда ∠1 = 4х.
Составим уравнение:
x + 4x = 180°
5x = 180°
x = 36°
∠2 = 36°
∠1 = 4 · 36° = 144°