Обозначим параллелограмм ABCD ,биссектриса проведена из угла В к стороне AD в точке M .Угол А =180°-150°=30°(сумма соседних углов параллелограмма 180°) .∠ABM равен углу BMC =150°÷2=75°(так как BM - биссектриса) .∠BMA треугольника ABM равен 180°-75°-30°=75°,значит треугольник ABM -равнобедренный с основанием BM ,поэтому AB=AM=16 см .AD=AM+MD=16+5= 21 см .Площадь параллелограмма ABCD найдём по формуле S=a×b×sinα(где а и b стороны параллелограмма ,а α-угол между ними).S=16×21×sin30°=336×0,5=168 см² .
Так как призма прямая и в основании квадрат, все углы между ребрами прямые. Между пересекающимися боковым ребром и диагональю основания, а так же пересекающимися стороной основания и диагональю боковой грани уголы прямые (если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой в этой плоскости, проходящей через точку пересечения). По теореме Пифагора находим: (17^2-15^2)=64 - квадрат диагонали основания. 64/2 = 32 - квадрат стороны основания. 32 + 15^2 = 32+225 =257 - квадрат диагонали боковой грани \|257 (см) - диагональ боковой грани
1.
Катеты фиолетового треугольника: 16; 6
Гипотенуза равна: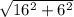
Гипотенуза фиолетового треугольника равна: 17.1.
2.
Чтобы найти наибольший катет бледно-красного, вычтим те 4 сантиметра с нашей гипотенузы: 17.1-4 = 13.1
Теперь к этому числу добавим те 9 сантиметров (в правой нижней стороне красного треугольника): 13.1+9 = 22.1
Теперь нам известно 2 катета бледно-красного треугольника: 22.1; 7.
Гипотенуза её равна:
Вычтим с этого числа те 2 сантиметров(в правом верхнем углу бледно-красного треугольника): 23.18-2 = 21.18.
3.
Теперь нам известна гипотенуза жёлтого треугольника, и его катет.
Второй катет равен: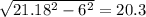
Теперь мы знаем 2 катета, и гипотенузу желтого треугольника.
4.
Прибавим к наибольшому катету 5 и 1(в правом и левом нижнем углу синего треугольника): 20.3+6 = 26.3.
Теперь нам известно 2 катета синего треугольника: 12; 26.3.
Гипотенуза равна: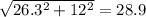 .
.
5.
Вычтим 11 сантиметров с гипотенузы синего треугольника (левый нижний угол зелёного треугольника): 28.9-11 = 17.9.
Теперь нам известно 2 катета зелёного треугольника: 14; 17.9.
Гипотенуза равна: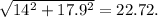
6.
Нам известна гипотенуза, и один катет розового треугольника: 16; 22.72.
Второй катет равен: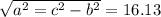 .
.
7. Прибавим к этому числу 5 сантиметров (нижний левый угол голубого треугольника): 16.13+5 = 21.13.
Теперь нам известно 2 катета: 5; 21.13
Найдём гипотенузу: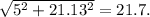
Вывод: самая верхняя гипотенуза равна 21,71 сантиметров.