
ответ: 25π (дм); 156,25π (дм²).
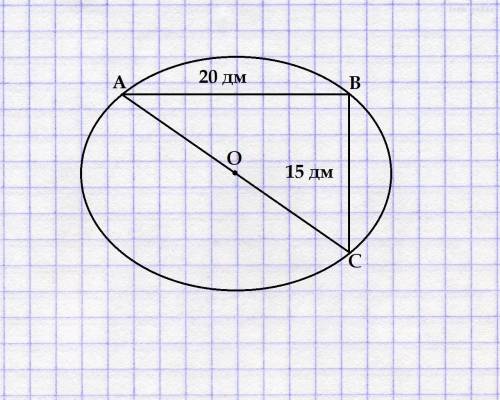
Объяснение: Для начала обратим внимание, что нам неизвестна гипотенуза.
Теорема Пифагора: сумма квадратов длин катетов равна квадрату длины гипотенузы.
⇒ c²=a²+b² ⇒ c=√(a²+b²)=√(15²+20²)=√(225+400)=√625=25 (дм).
НО можно было не вычислять поскольку есть такое понятие пифагорова тройка, которая содержит пифагоровые числа, удовлетворяющие соотношению Пифагора.
Поэтому мы могли сразу написать по табличке, что:
| a | b | c |
| 15 | 20 | 25 |
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Т.к. AC - диаметр окружности с центром в точке О ⇒ R=25/2=12,5 (см).
Сразу найдём теперь и длину окружности, и площадь круга.
C=2π12,5=25π (дм); S=π12,5²=156,25π (дм²).
Відповідь:
75°, 21° та 84 °
Пояснення:
По-перше знайдемо кут суміжний відомому зовнішньому: 180-105=75°
То ж один кут = 75°, другий кут позначимо просто Х, а третій кут, той що в 4 рази більший, позначимо 4*Х.
Відомо, що сума всіх внутрішніх кутів будь-якого трикутника = 180°.
Запишемо математичну модель до задачі, використовуючі умовні позначення сторін:
75 + Х + 4Х = 180
Х + 4Х = 180 - 75
5Х = 105
Х = 21
Другий кут = 21°, а третій кут буде 4 * 21° = 84°.
Перевіримо наші відповіді:
75°+21°+84°=180°
Рішення вірне!
Объяснение:
1) АД и ВД гипотезы равных прямоугольных треугольников т.к. в основании правильный ∆ (АС=ВС по условию;СД--общая; СД и ∆АВС перпендикулярны по условию =>
АД=ВД=√(СД^2+АС^2)
АД =ВД = √((16√3)^2+16^2)=32
2). АК и ВК ∆АОК и ∆ВОК
т.к. ∆АВС равносторонний медиана является биссектрисой и высотой
=> ОА=ОВ = 2/3 от длины медианы
ОК общая => ∆АОК =∆ВОК => АК=ВК
∆АВО равнобедренный основание АВ=16√3. <АОВ=120°; ОА=ОВ
АВ^2= 2ОА^2 - 2*АО^2*Cos120°
АВ^2 = 2АО^2(1-Cos120°)
АО^2 = АВ^2/(2*(1-Cos120°)
АО^2 = (16√3)^2/ (2*(1-Cos120°))
АК=ВК = √( ОК^2 + АО^2)
ОК ^2= 12^2= 144
Представляем и считаем, арифметику самостоятельно.