92,8 см
Объяснение:
Так как MNKL - прямоугольник, то его противоположные стороны попарно равны: MN = KL, NK = ML.
Диагонали прямоугольника равны: МК=NL.
Q, R, S и T - середины сторон прямоугольника ⇒
MQ=QN=KS=SL, NR=RK=MT=TL.
Средняя линия треугольника — отрезок, который соединяет середины двух сторонQR - средняя линия ΔMNK, RS - средняя линия ΔNKL, TS-средняя линия ΔMKL, QT- средняя линия ΔNML.
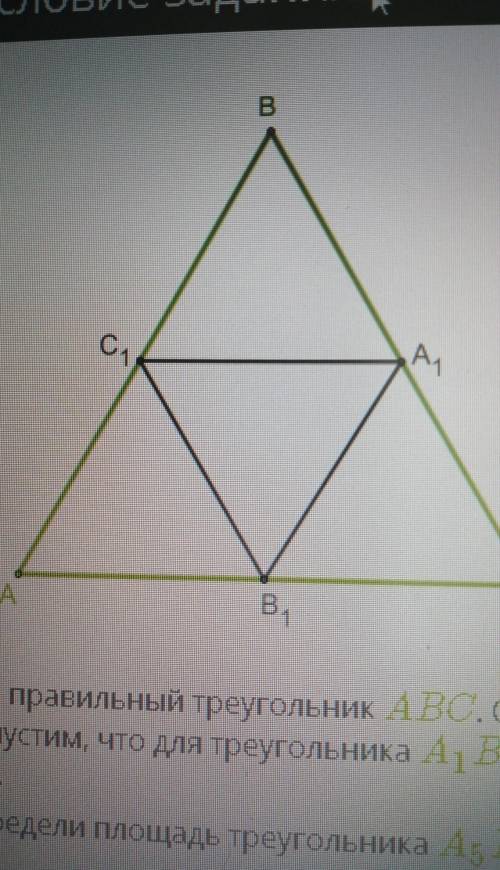
Средняя линия параллельна третьей стороне, а ее длина равна половине длины этой стороныQR =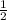 
* МК = * 46,4 = 23,2 см
TS = * МК = 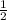* 46,4 = 23,2 см
RS = 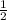* NL = 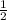* 46,4 = 23,2 см
QT = 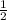* NL = 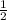* 46,4 = 23,2 см
Периметр четырёхугольника QRST:
Р=QR+TS+RS+QT=4*23,2=92,8 см
Sabc = 30 см².
Объяснение:
Если условие такое: "В треугольнике ABC, ∠C = 45°, а высота ВН делит сторону AC на отрезки СН и НA соответственно равные 5 см и 7 см. Найдите площадь треугольника ABC", то решение:
Площадь треугольника АВС равна половине произведения высоты на сторону, к которой проведена эта высота.
Так как сторона АС, к которой проведена высота ВН, равна СН+НА = 5 + 7 = 12 см, а высота ВН = НС = 5 см (так как прямоугольный треугольник ВНС с углом С равнобедренный) то площадь треугольника АВС равна:
Sabc = (1/2)BH·AC = (1/2)·5·12 = 30 см².