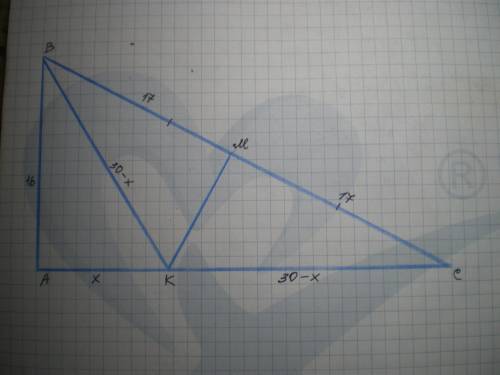
Дано: ΔАВС - прямокутний, ∠А=90°, АС=30 см, ВС=34 см; МК⊥ВС, ВМ=МС. Знайти МК.
Знайдемо АВ за теоремою Піфагора:
АВ=√(ВС²-АС²)=√(1156-900)=√256=16 см.
Проведемо ВК і розглянемо ΔВКС - рівнобедрений, тому що ВМ=СМ і МК⊥ВС, отже ВК=КС.
Нехай АК=х см, тоді КС=ВК=30-х см.
Знайдемо АК з ΔАВК - прямокутного:
АВ²=ВК²-АК²; 16² = (30-х)² - х²; 256=900-60х+х²-х²;
60х=900-256=644; х=10 11/15 см. АК=10 11/15 см, тоді
ВК = 30 - 10 11/15 = 19 4/15 = 289/15 см.
Знайдемо МК за теоремою Піфагора з ΔВМК, де ВМ=34:2=17 см.
МК²=ВК²-ВМ²=(289/15)² - 17² = (83521/225) - 289 = 18496/225.
МК=√(18496/225)=136/15=9 1\15 см.
Відповідь: 9 1/15 см.
Теорема 1. В треугольнике против большей стороны лежит больший угол.
Доказательство. Пусть в треугольнике ABC сторона АВ больше стороны АС (рис.1, а).
Рис.1
Докажем, что ∠ С > ∠ В. Отложим на стороне АВ отрезок AD, равный стороне АС (рис.1, б). Так как AD < АВ, то точка D лежит между точками А и В. Следовательно, угол 1 является частью угла С и, значит, ∠ C > ∠ 1. Угол 2 — внешний угол треугольника BDC, поэтому Z 2 > Z В. Углы 1 и 2 равны как углы при основании равнобедренного треугольника ADC. Таким образом, ∠ С > ∠ 1, ∠ 1 = ∠ 2, ∠ 2 > ∠ B. Отсюда следует, что ∠ С > ∠ В.
Справедлива и обратная теорема (ее доказательство проводится методом от противного).
Теорема 2. В треугольнике против большего угла лежит большая сторона.
Из теоремы 1 вытекает
Следствие 1. Если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника).
Доказательство следствия проводится методом от противного.
Из следствия 1 следует, что если три угла треугольника равны, то треугольник равносторонний.
Из теоремы 2 получаем
Следствие 3. В прямоугольном треугольнике гипотенуза больше катета.
С использованием теоремы 2 устанавливается следующая теорема.
Теорема 3. Каждая сторона треугольника меньше суммы двух других сторон.
Следствие 4. Для любых трех точек А, В и С, не лежащих на одной прямой, справедливы неравенства:
АВ < АС + СВ, АС < АВ + ВС, ВС < ВА + АС.
ответ: АС=44дм; СВ=44дм; АС=55дм.
Объяснение: Для решения этой задачи примем длины боковых сторон за х, длина основания будет х+11. Cоставим уравнение вида:
х+х+(х+11)=143 дм; решая уравнение получим: 3х=143-11=132дм;
х=44дм - длина боковоых сторон АВ и СВ;
Находим АВ=44+11=55дм.