Объем пирамиды равен одной трети произведения ее высоты на площадь основания.
V=⅓ S∙h
Основание правильного шестиугольника состоит из шести правильных треугольников.
Площадь правильного треугольника находят по формуле:
S=(а²√3):4
S=4√3):4=√3
Площадь правильного шестиугольника в основании пирамиды:
S=6√3
Высоту найдем из прямоугольного треугольника АВО:
Так как ребро образует с с диагональю основания угол 60°, высота пирамиды ВО равна
H=ВО=2:ctg (60°)= 2·1/√3=2√3
Можно найти высоту и по т. Пифагора с тем же результатом.
V= 2√3∙6 √3:3=12 (кубических единиц)
Подробнее - на -
Объяснение:
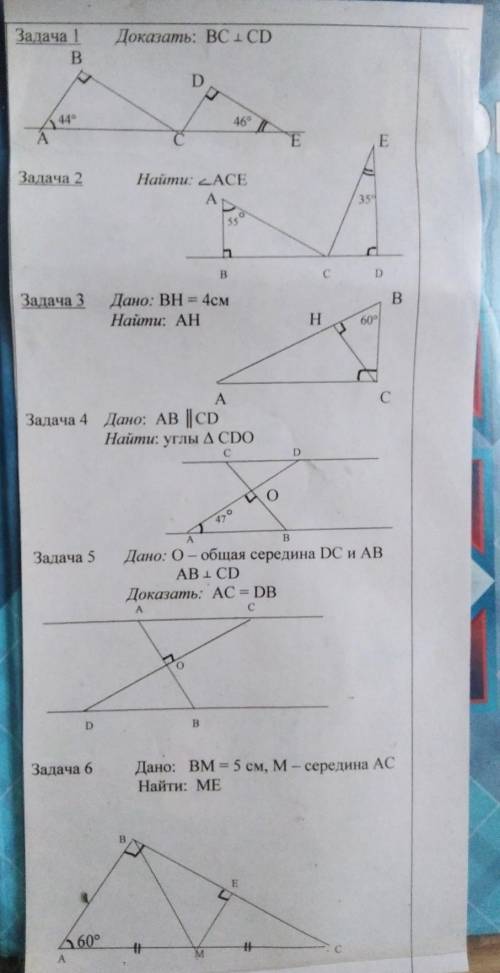
Нехай маємо прямокутний трикутник ABC (∠C=90), у якого AC=√5 см – катет і BH=4 см – проекція катета BC на гіпотенузу AB (за умовою).
прямокутний трикутник, рисунок Проведемо висоту CH=h до гіпотенузи AB (AB⊥CH).
За властивістю прямокутного трикутника
h^2= AH•BH
(це виводиться із подібності прямокутних трикутників ABC і CBH).
Нехай AH=x - проекція катета AC на гіпотенузу AB, тоді h^2=4x.
У прямокутному ΔACH (∠AHC=90), у якого AH=x і CH=h=2√x – катети, AC=√5 см – гіпотенуза, за теоремою Піфагора запишемо:
AH^2+CH^2=AC^2, x^2+4x=5, x^2+4x-5=0,
за теоремою Вієта, отримаємо
x1=1 і x2=-5<0, звідси AH=1 см.
AB=AH+BH=1+4=5 см – гіпотенуза ΔABC.
Відповідь: 5.
3.
<B = 60° => <HCB = 90-60 = 30° .
Теорема 30-градусного угла прямоугольного треугольника такова: сторона, противолежащая 30-и градусам в прямоугольном треугольнике — равен половине гипотенузы, тоесть: HB = 4 => BC = 4*2 = 8.
<B = 60° => <A = 90-60 = 30°.
По той же теореме следует это: BC = 8 => AB = 8*2 = 16.
HB = 4 => AH = 16-4 = 12.
Вывод: AH = 12.
4.
<OAB & <CDO — пара накрест лежащих углов, так ка прямые параллельны, то накрест лежащие углы друг другу равны, тоесть: <CDO = 47°.
<AOB = 90° => <COD = 90° (так как вертикальные углы).
<COD = 90°; <CDO = 47° => <DCO = 90-47 = 43°.
Вывод: <CDO = 47°; <DCO = 43°; <COD = 90°.
5.
Тема: Равенство треугольников.
По какому-то там признаку (не помню номер) — если 3 угла из каждого треугольника равны, то треугольники также друг другу равны.
Определим же эти углы: Так как прямыеу паралелльны, то накрест лежащие углы равны, тоесть: <ODB == <ACO. Нашл первую пару равных углов!
Вторая пара накрест лежащих друг другу равных углов: <CAO; <OBD.
Вторую пару то определили.
Так как <AOC = 90°, то его вертикальный угол — <DOB — также равен 90 градусам.
Доказали, что в двух треугольниках имеется 3 определения углов, что и означает, что треугольники равны.
И так как треугольники равны, то OB == AO; DO == OC.
Так как треугольники имеют 2 общей стороны, то против вертикальных прямых углов — лежат другу другу равные стороны — DB; AC.
6.
<A = 60° => <C = 30°.
По теореме 30-грдусного угла — катет AB — равен половине гипотенузы AC.
BM — медиана, потому что делит гипотенуз пополам, и также медиана прямоугольного треугольника, проведёнаня к гипотенузе — равна её половине, тоесть: BM == MC == AM = AC/2 = 5 => AC = 5*2 = 10.
BM == MC => <MBE == <MCE = 30° (<C = 30°).
<EMC = 90°; <C = 30° => <ME = MC/2 = 5/2 = 2.5.
Вывод: ME = 2.5.