∠CDE составляет одну часть, ∠ADE - 8 таких частей, всего 9 частей.
∠CDE = 90° : 9 = 10°
Сумма острых углов прямоугольного треугольника 90°, тогда из ΔCDE:
∠DCE = 90° - ∠CDE = 90° - 10° = 80°
Диагонали прямоугольника равны и точкой пересечения делятся пополам, тогда ΔCOD равнобедренный (CO = OD), значит углы при его основании равны:
∠OCD = ∠ODC = 80°.
В ΔOCD находим третий угол:
∠COD = 180° - (∠OCD + ∠ODC) = 180° - 160° = 20° - угол между диагоналями.
Объяснение:
Подпишись на меня в ютубе мой канал. LIXORADKA 43. Буду тебя там ждать)
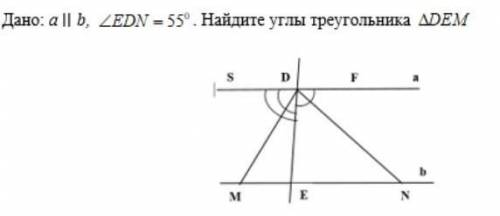
<EDN == <NDF => <FDE = 55*2 = 110° =>
<SDE = 180-110 = 70°
По первому признаку параллельности прямых — накрест лежащие углы равны, тоесть: <FDE == <DEM = 110°.
<SDM == <DMK => <DMK = 70/2 = 35° => <DME = 180-(110+35) = 35°.
Вывод: <DME == <DMK = 35°; <DEM = 110°.