Кокружности проведена касательная ав (в-точка касания). прямая ам проходит через центр окружности и пересекает ее в точках м и n. найти квадрат расстояния от точки в до прямой an, если ам=1, ав равнен корень квадратный
из 3 в правильном шестиугольнике abcdef из вершины с на диагональ ad опущен перпендикуляр ск. найти отношение длин отрезков ак и kd в трапеции abcd с основаниями ad и вс длина средней линии mn =10. площади четырёхугольников
mbcn и amnd относятся как 3: 5 соответственно. во сколько раз длина ad больше длины вс?
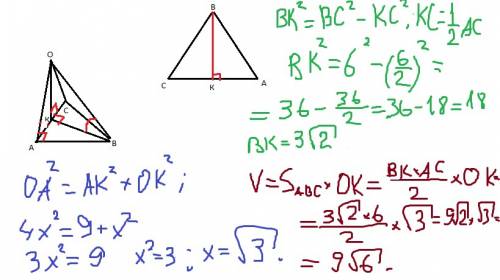
1. AN = AB^2/AM = 3; MN = 2; => OB = 1;
=> угол BAO = 30 градусов; BH = AB*sin(30) = корень(3)/2;
2. О - центр правильного шестиугольника.
ОС = ОD = CD = OA; => OK = KD; => AK/KD = 3;
3. вот тут есть кое-что интересное. Построение такое - проводим ВР II CD, Р лежит на MN. Проводим PK II BA, K лежит на AD. Ясно, что PN = BC; => MP = (AD - BC)/2 = AK;
Трапеция KPND равна трапеции MBCN, то есть её площадь составляет 3/5 площади AMNP. Площадь параллелограмма AMPK, соответственно, составляет 2/5 от площади AMNP. Поскольку у этих фигур общая высота, отношение их площадей равно отношению средних линий.
Обдумайте это внимательно - речь идет о средних линиях параллелограмма (а параллелограмм - частный случай трапеции :)) AMPK, равной АК = МР = (AD - BC)/2; и средней линии трапеции KPND, то есть - трапеции MBCN, равной ((AD + BC)/2 + BC)/2 = (AD/4 + 3*BC/4);
(Я вынужден сделать замечание. Условие MN = 10 я намеренно не использую, хотя отлично вижу, что тут можно было бы подставить это значение.)
Итак, получилось (AD/2 + 3*BC/2)/(AD - BC) = 3/2; обозначим AD/BC = x;
(x/2 + 3/2)/(x - 1) = 3/2; x = 3;
Условие MN = 10 позволяет найти основания, равные 5 и 15.