Тогда площадь нашего параллелограмма равна 9 см×2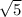 дм = 0,9 дм×2
дм = 0,9 дм×2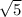 дм = 1,8
дм = 1,8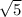 дм².
дм².
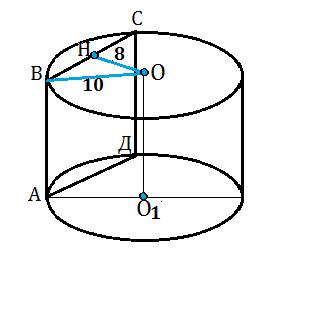
ответ:В задачах этого параграфа двугранный угол с ребром АВ, на разных гранях которого отмечены точки С и D, для краткости будем называть так: двугранный угол CABD.
Дано: ABCD - тетраэдр;
Определим линейную меру двугранного угла DACB.
ADC ⊥ пл. АВС, тогда двугранный угол DACB и соответствующий ему линейный угол DCB равны 90о.
Определим линейную меру двугранного угла DABC.
Проведем отрезок СМ ⊥ АВ, соединим точки М и D.
то по теореме о 3-х перпендикулярах,
По определению, ∠DMC - линейный угол двугранного угла DABC.
По теореме Пифагора:
Тогда
Отсюда
Определим линейную меру двугранного угла BDCA.
то ∠АВС - линейный угол двугранного угла
Объяснение:
180кор5 см² (или если в дециметрах 1.8кор5 дм²)
Объяснение:
Площадь параллелограмма равна S=ah, где h - высота, а- сторона, к которой эта высота проведена. В 1 дм=10см. Мы можем перевести 9см=0.9 дм. Тогда S=0,9×2кор5=1.8кор5 дм²
Так же мы можем перевести 2кор5 дм=20кор5 см. Тогда S=9×20кор5=180кор5 см²
Эти два ответа одинаковы, просто выражены в разных величинах