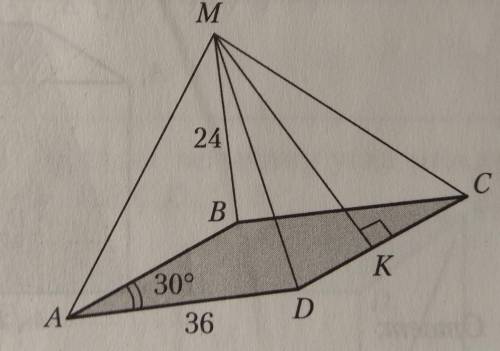
По условию данные две прямые не имеют общих точек с прямой а и пересекаются в т.М, значит, лежат в одной плоскости (свойство). Прямые в пространстве могут пересекаться, быть параллельными или скрещивающимися. Предположим, что ни одна из этих прямых не является скрещивающейся с прямой а. Так как они не пересекают прямую а ( не имеют с ней общих точек). обе параллельны прямой а. Но это допущение противоречит
Аксиоме параллельных прямых. Через любую точку, лежащую вне прямой, можно провести другую прямую, параллельную данной, и притом только одну.
⇒ Данные прямые не могут обе быть параллельными прямой а, поэтому хотя бы одна из них является скрещивающейся с прямой а
M - точка пересечения медиан
Медианы делятся точкой пересечения 2:1 от вершины.
AM:MD =CM:MK =2:1
AM=10; MD=5; CM =4; MK=2
Определим, какая из сторон ABC равна 6.
В треугольнике сумма двух сторон всегда больше третьей (неравенство треугольника).
△AMC: AC+CM>AM => AC>10-4 => AC>6
△AMK: AK+MK>AM => AK>10-2 => AK>8 => AB>8
Следовательно только сторона BC может быть равна 6.
BC=6, CD=3, △MDC - египетский (3:4:5) => BCK=90°
△BCK: BC=CK=6; BK=6√2 (т Пифагора) => AB=12√2
Продлим BC, AE||CK, E=90
△BEA~△BCK, k=AB/BK =2
CE=BC=6; AE=2CK=12
△ACE: AC =√(AE^2 +CE^2) =6√5