1)Из центра O окружности, вписанной в трапецию, восстановлен перпендикуляр OM к плоскости трапеции.
Найдите радиус окружности, если расстояния от точки M до одной из сторон трапеции и до ее плоскости равны 3 см и 3,4 см.
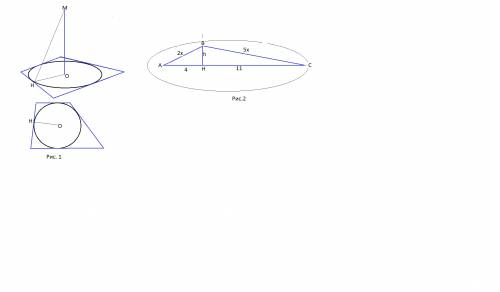
Сделаем рис.№1. Обозначим расстояние от М до стороны трапеции МН.
Расстояние между точкой и плоскостью измеряется длиной отрезка, перпендикулярного плоскости.
Следовательно, ОМ=3 cм, а расстояние МН от М до стороны трапеции=3,4 cм, так как перпендикуляр всегда короче наклонной, а МН - наклонная, проведенная перпендикулярно стороне трапеции. Любой стороне.
Ее проекция ОН также будет перпендикулярной этой стороне ( теорема о трех перпендикулярах).
Причем это относится к любой стороне трапеции - перпендикуляр из О к стороне трапеции пересекает ее в точке касания окружности и стороны, являющейся в данном случае касательной к окружности.
Этот перпендикуляр - проекция расстояния от М до стороны - и будет радиусом вписанной окружности. Найдем его по т. Пифагора:
ОН= √(МН²-ОМ²)=1,6 см
ответ: Радиус окружности равен 1,6 см
2) Из одной точки к плоскости проведены перпендикуляр и две наклонные, проекции которых равны 4 и 11 см.
Найдите длину перпендикуляра, если наклонные относятся как 2:5
Сделаем рисунок №2,
обозначим вершины получившейся фигуры привычными А, В, С.
Рассмотрим треугольник АВС, который образован наклонными АВ и ВС и их проекциями АН и НС.
Высота ВН- искомый перпендикуляр- может быть найдена из треугольников АВН и ВСН.
Выразим ее значение из этих треугольников по т.Пифагора.
ВН²=АВ²-АН²
ВН²=ВС²-НС²
Приравняем эти значения:
АВ²-АН²=ВС²-НС²
Пусть коэффициент отношения наклонных равен х. Тогда
4х²-16=25х²-121
21х²=105
х²=5
х=√5
ВН²=АВ²-АН²
ВН²=20-16=4
ВН= √4=2 см
ответ: Длина перпендикуляра - 2 см
Вариант 1: АС = √13 см.
Вариант 2: АС = 5 см.
Объяснение:
В треугольнике АВС АВ=3√2, ВС=1, АС=√2*R (дано). Найти АС.
По теореме синусов: АС/sinB = 2R. => R√2/SinB = 2R.
SinB = √2/2. Значит угол равен 45 градусов и cosB=√2/2. По теореме косинусов:
АС²= АВ²+ВС² - 2АВ*ВС*cosB. Подставляем значения и получаем
АС² =18+1 - 2*3√2*1*√2/2 =13.
АС = √13 см.
Второй вариант:
Угол при вершине В тупой и тогда косинус этого угла отрицательный и равен -√2/2. Тогда
АС²= АВ²+ВС² + 2АВ*ВС*cosB = 18+1 + 6 =25.
АC = √25 = 5 см.
Проверка по теореме о неравенстве треугольника:
Вариант 1: АВ≈4,24; ВС=1; АС≈3,6. 4,24 < 3,6+1. Треугольник существует.
Вариант 2: АВ≈4,24; ВС=1; АС=5. 5 < 4,24+1. Треугольник существует.