Дано :
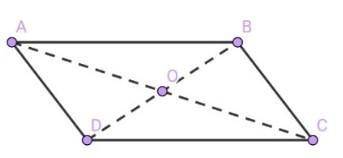
Четырёхугольник ABCD — параллелограмм.
AD = 30.
Отрезки BD и AC — диагонали.
АС = 43.
BD = 35.
Найти :
S(ABCD) = ?
Диагонали параллелограмма, пересекаясь, делятся пополам и образуют четыре равновеликих (равных по площади) треугольника.То есть —
AO = OC = 43 : 2 = 21,5.
DO = OB = 35 : 2 = 17,5.
S(∆AOD) = S(∆AOB) = S(∆BOC) = S(∆DOC).
Рассмотрим ∆AOD.
Найдём его площадь по формуле Герона —
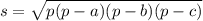
Где s — площадь треугольника; р — полупериметр (одна вторая суммы сторон треугольника) треугольника; а, b и с — длины сторон треугольника.
Найдём р ∆AOD.
p(∆AOD) = 0,5*(AO + DO + AD) = 0,5*(21,5 + 17,5 + 30) = 0,5*69 = 34,5.
Теперь подставляем всё в формулу Герона —
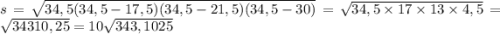
По выше сказанному S(ABCD) =
(10√343,1025) * 4 = 40√343,1025 (ед²).
40√343,1025 (ед²).
Надо знать что сторона лежащая против большого угла, самая большая сторона в треугольнике ( при условии что он не равностороний, в нашем случае не так) .
Запишем неравенство:
Понятно что если ∠P>∠N и ∠O>∠P то ∠O>∠N
Отсюда следует, что самая длинная сторона, находится против большого ∠O (сторона NP)
∠P>∠N
Значит против ∠Р лежит сторона, большая от стороны против угла N
И меньшая стороне NP.
В итоге получаем:
NP>ON>OP
Данное утверждение правильно, так как углы не равны, а значит и стороны не равны.