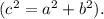Объяснение:
а) Пусть СХ=х , тогда ХД=7-х.
Произведение отрезков одной хорды равно произведению отрезков другой хорды ⇒
СХ*ХД=АХ*ХВ,
х*(7-х)=2*6 , 7х-х²=12 ,
х²-7х+12=0, D=49-48=1>0 ,
По т. Виета х₁+ х₂=7
х₁* х₂=12 ⇒ х₁=4, х₂=3 .
Если СХ=4 , тогда ХД=7-4=3.
Если СХ=3 , тогда ХД=7-3=4.
б) ∪ АД=80°, ∪ СВ=48°.∠АХС=180°-∠АХД. Найдем угол ∠АХД по теореме : "Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами " ⇒
∠АХД=(48°+80°):2=64°.
∠АХС=180°-64°=116°.
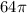см³.
Объяснение:Обозначим данную пирамиду буквами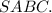
Проведём высоту пирамиды SO.
Начертим около этой пирамиды конус.
Так как конус описан около данной пирамиды, то высота конуса совпадает с высотой данной пирамиды.
=======================================================
Так как данная пирамида - правильная, треугольная ⇒ основание данной пирамиды - правильный треугольник.
Проведём высоту
в 
Так как
- равносторонний ⇒ 
- высота, медиана и биссектриса
Найдём
по теореме Пифагора 
.
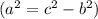Точка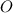
- пересечение медиан и делит их в отношении 
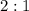, считая от вершины.
Также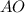
- радиус описанной около 
окружности.
Рассмотрим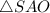
Если угол в прямоугольном треугольнике равен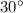
, то напротив лежащий катет равен половине гипотенузы.
Составим уравнение:
Пусть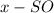
, тогда 
.
И по теореме Пифагора