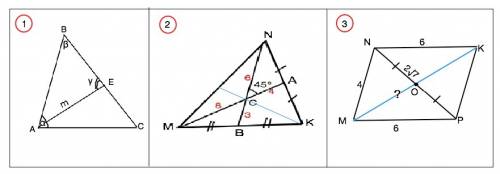
1) Медианы треугольника точкой пересечения делятся в отношении 2:1, считая от вершины. ⇒ NC:СВ=6:3, и MC:СА=8:4. Одна из формул площади треугольника S=a•b•sinα•1/2, где а и b - стороны, α- угол между ними. Sin45°=√2/2, Тогда Ѕ(ACN)=6•4•√2/2=6√2. Медиана делит площадь треугольника пополам, три медианы делят его на 6 равновеликих треугольника. S(MNK)=6•Ѕ(ACN)=36√2 (ед. площади)
2) В ∆ АЕС по теореме синусов АЕ:sin∠С=АС:sin∠АЕC. Сумма углов треугольника 180°. В ∆ АВС ∠С =180°-(α+ β). ∠АЕС=180°-γ. ⇒ m:sin(180°-α- β)= =AC:sin(180°-γ), откуда АС=m•sin(180*-γ)/sin(180*-α-β).
3) Диагонали параллелограмма точкой пересечения делятся пополам. ⇒ В треугольнике МNP отрезок МО - медиана. Формула медианы произвольного треугольника М=(√(2a²+2b²-c²):2, где а и b - стороны, с - сторона, которую медиана делит. ⇒ МС=2МО=√(32+72-28)=2√19 ед. длины.
Или
Из ∆ МNP по т.косинусов NP²=MN²+MP²-2•MN•NP•cosNMP ⇒ MP²=16+36-48•cosNMP ⇒ cosNMP=(28-52):(-48)=1/2
По т.косинусов МК²= MN²+NK²-(-2•MN•NK•cos∠MNK). Сумма соседних углов параллелограмма 180° (т.к. МР||NK, MN - секущая, угол NMP и угол MNK- внутренние односторонние). ⇒cosMNK= - cosNMP ⇒ МК=√(52+24)=2√19 (ед. длины)
Теорема косинусов для треугольника AМC
AC^2=AM^2+MC^2-2*AM*CM*cosAMC
Теорема косинусов для треугольника BМC
BC^2=BM^2+MC^2-2*BM*CM*cosBMC
AC=BC (треугольник равносторонний) Тогда AC^2=BC^2
AM^2+MC^2-2*AM*CM*cosAMC=BM^2+MC^2-2*BM*CM*cosBMC
AM^2-2*AM*CM*cosAMC=BM^2-2*BM*CM*cosBMC
АМ и ВM знаем
2^2-2*2*CM*cosAMC=10^2-2*10*CM*cosBMC
4-4*CM*cosAMC=100-20*CM*cosBMC
Углы ВМС и ВАС равны, опираются на одну дугу. ВАС=60 - равносторонний треугольник.
Угол АМС=АМВ+ВМС=АСВ+ВАС=60+60=120
4-4*CM*cos120=100-20*CM*cos60
4-4*CM*(-1/2)=100-20*CM*1/2
4+2*CM=100-10*CM
12*CM=96
СМ=8
ответ: 8
вроде так
Объяснение: