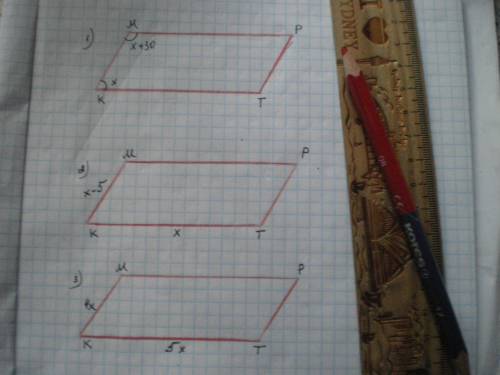
1. Сумма углов параллелограмма, прилегающих к одной стороне, составляет 180°.
Пусть ∠К=х°, тогда ∠М=х+30°. Составим уравнение:
х+х+30=180; 2х+30=180; 2х=150; х=75.
∠К=75°, ∠М=75+30=105°.
∠Р=∠К=75°; ∠Т=∠М=105° как противолежащие углы параллелограмма.
2. Полупериметр р (КМРТ)=400:2=200 см. Пусть КТ=х см, тогда КМ=х-5 см. Составим уравнение:
х+х-5=200; 2х=205; х=102,5;
КТ=102,5 см; КМ=102,5-5=97,5 см;
МР=КТ=102,5 см;
РТ=КМ=102,5-5=97,5 см. (как противолежащие стороны параллелограмма)
3. Периметр КМРТ=180 см. Пусть КМ=4х см, КТ=5х см. Составим уравнение:
(4х+5х)*2=180; 9х*2=180; 18х=180; х=10.
КМ=10*4=40 см, КТ=10*5=50 см; РТ=КМ=40 см; МР=КТ=50 см. (как противолежащие стороны параллелограмма).
Решение
Найдём угол В (ну или угол АВС, это одно и то же). По свойству внешнего угла он равен 180° - 140° = 40°
Угол А = угол С (св-во равнобедренного треугольника)
Угол А + угол В + угол С = 180° (теорема о сумме углов треугольника)
Отсюда, угол А = (180° - 40°)/2 = 70°. Угол С также равен 70°
70° > 40°. Воспользуемся неравенством треугольника (против большего угла лежит большая сторона и обратно: против большей стороны лежит больший угол). Так как угол В — наименьший угол, а также угол при вершине, против которого лежит сторона АС, то сторона АС — наименьшая.
ответ: б)