
Объяснение:
10)
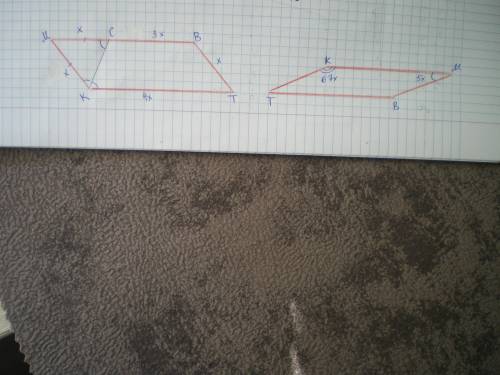
Дано: КМВТ - параллелограмм, Р=65 см, КС - биссектриса, МС/ВС=1/3.
Найти МВ.
∠МКС=∠СКТ по определению биссектрисы
∠СКТ=∠МСК как внутренние накрест лежащие при МВ║КТ и секущей КС
значит, ΔМКС - равнобедренный и МК=МС.
Пусть МС=МК=ВТ=х см, тогда ВС=3х см, КТ=МВ=х+3х=4х см.
Составим уравнение: х+х+4х+4х=65
10х=65; х=6,5
МВ=КТ=6,5 * 4 = 26 см.
ответ: 26 см.
11)
Дано: КМВТ - параллелограмм ∠М/∠К=5/67. Найти ∠К.
Сумма углов параллелограмма, прилегающих к одной стороне, составляет 180°.
Пусть ∠5х°, тогда ∠К=67х°.
Составим уравнение:
5х+67х=180; 72х=180; х=2,5
∠К=67*2,5=167,5°
ответ: 167,5°
(x - x1)/a = (y-y1)/b = (z - z1)/c
Коэффициенты а, b, с - это координаты направляющего вектора, а числа x1, y1, z1 - это координаты точки, через которую проходит прямая.
В данной задаче направляющий вектор является нормальным вектором к заданной прямой: s(2, -1, 3)
Таким образом, мы знаем координаты вектора, перпендикулярного искомой прямой (перпендикуляра) .
Теперь вспомним еще один вид уравнения прямой:
Ax + By + Cz + D = 0
В этом уравнении коэффициенты A, B, C -это координаты нормального вектора, т. е. вектора перпендикулярного этой прямой. Но ведь мы уже знаем координаты перпендикулярного вектора! ! То есть, мы знаем почти все уравнение:
2x - y + 3z + D = 0
Однако надо найти коэффициент D. А это сделать очень просто: дело в том, что точка А (2,3,1) по условию лежит на данной прямой. Так что если подставить её координаты в уравнение прямой, уравнение обратится в тождество. Подставим:
2*2 - 3 + 3 + D = 0
4 + D = 0
D= -4
ответ: искомое уравнение перпендикуляра: 2х - у + 3z - 4 = 0