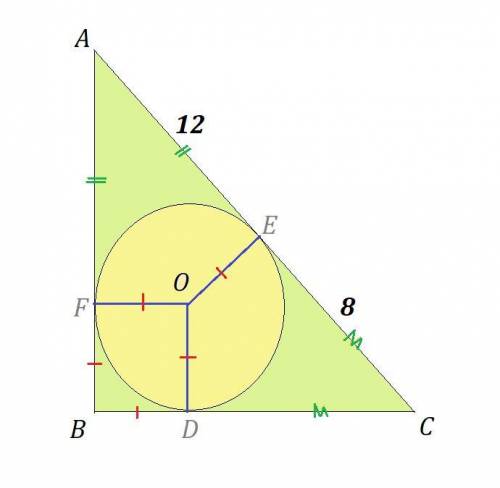
Дано:
ΔABC, ∠B = 90°.
Вписанная окружность с центром O и радиусом OD = OE = OF,
D∈BC, E∈AC, F∈AB.
OE = 12 (см), EC = 8 (см).
Найти:
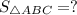
Заметим, что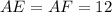 
и 
(так как отрезки касательных, проведенных к окружности из одной точки, равны).
Пусть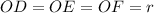 
.
Тогда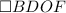 
- квадрат, так как 
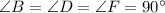(и, значит, 
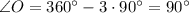), а также 
, 
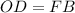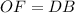и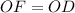 
. - Все стороны и углы данного четырехугольника равны.
Значит,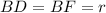 
.
Тогда катеты треугольника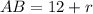 
и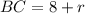 
, а гипотенуза равна 
.
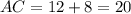По тереме Пифагора:
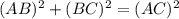
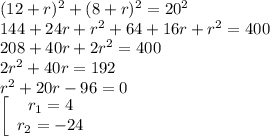
Второй корень нам не подходит (он отрицательный ... ).
Так что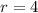 
.
Можем найти площадь:
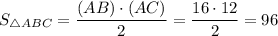
Задача решена!
96 см².
Высота равностороннего треугольника равна 25√3. Найдите его периметр.
Решение:
1) Так как треугольник равносторонний, то ∠A = ∠B = ∠C = 180° : 3 = 60°.
2) Рассмотрим треугольник ABH (∠H = 90)
∠B = 180° - 90° - 60° = 30°
3) AH = половине AB = AB/2 - Катет, лежащий против угла в 30°.
AB2 = (25√3)2 + (AB/2)2
AB2 = 1875 + AB2/4
AB2 - AB2/4= 1875
(3AB2)/4 = 1875
Крест-накрест:
3AB2 = 4 * 1875
3AB2 = 7500
AB2 = 7500 / 3
AB2 = 2500
AB = √2500
AB = 50
4) Периметр равен сумме всех сторон, так как треугольник имеет 3 стороны и в данном случа они все равны, то:
P = 50 + 50 + 50 = 150
ответ: 150