а) 8 см; б) 18 см
Объяснение:
знаходимо відстань від прямої до вершини похилих
за теоремою Піфагора
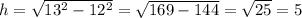
знаходимо відстань від основи перпедикуляра до основи другої
похилої = h (кут нахилу =45, відповідний трикутник рівнобедренний,
отже проекція другої похилої = відстані до прямої від вершини похилих)
l2 = 5
l1 = 13 за умовою
це відстані від основи перпедикуляра до основ другої та першої похилої.
а)
якщо похилі лежать по один бік від основи перпендикуляра, то відстань = 13-5 = 8 см
б)
якщо похилі лежать по різні боки від основи перпендикуляра, то відстань = 13+5 = 18 см
Вычисляем для начала длину медианы треугольника, обозначим её за m.
В правильном (равностороннем) треугольнике m=(√3/2)*a, где a- сторона треугольника.
m=(√3/2)*12=6√3 см
Далее воспользуемся следующим свойством медиан треугольника:
"Медианы треугольника пересекаются в одной точке (называемой центроидом), и делятся этой точкой на две части в отношении 2:1, считая от вершины"
Таким образом меньший участок медианы равен:
6√3/3=2√3
И теперь по теореме Пифагора находим нужное расстояние (рисунок уж я не стал делать...):
√((2√3)²+2²)=√(12+4)=√16=4 см