Дано:
ДАВС - равносторонний
ВН=9 см
Найти:
S=? см2
Решение
Площадь треугольника равна:
S=1/2×AC×BH, где
AC - длина основания, AC=AB=BC (у
равностороннего треугольника)
ВН - высота
Пусть АС=2а см, тогда
АН=1/2×АС=1/2×2а=а см.
По теореме Пифагора:
AB2=BH2+AH2
(2a)2=92+a2
4a2-a2=81
3a2=81
a2=81=3
a2=27
a=1/27=~/9×3=3+/3 см
Площадь равна:
S=1/2×9×3-V3=1/2×27/-v3=27-/3/2=13,5-v3
см2
ОТВЕТ: площадь равна 13,5 /3 см2
ответ:
объяснение:
1. вк=ав/2, значит вк= 1/2, а вк перпендикульярна ад, следовательно угол а = 30 гр. (т.к. если катет равен половине гипотинузы то угол лежащий против этого катета равен 30 гр.)
угол а=углу с, т.к. авсд - параллелограмм.
угол авк=60 гр., а
угол в = 60+90=150 гр. угол в= углу д
2.
авсд-трапеция
ад-?
из вершины с проводим перпендикуляр се
решение
ав=вс=10(за условием)
ав=се=10(по свойству)
∠е=90° ⇒ ∠д=∠с=45°⇒δсед-прямоугольный(∠е=90°)
се=ед=10 ⇒ δсед-равнобедренный
ад=ае+ед(при условии)
ад=10+10=20 см
ад=20 см
3.
дано: ромб abcd
угол а = 31°
решение:
в ромбе диагонали являются биссектрисами =>
=> 31/2=15.5 - угол оаd
диагонали пересекаются под прямым углом =>
=> угол аоd = 90°
сумма углов треугольника равна 180° =>
=> 180-90-15.5=74.5° - угол аdo
отв: 74.5°, 90°, 15.5°
4
на фото
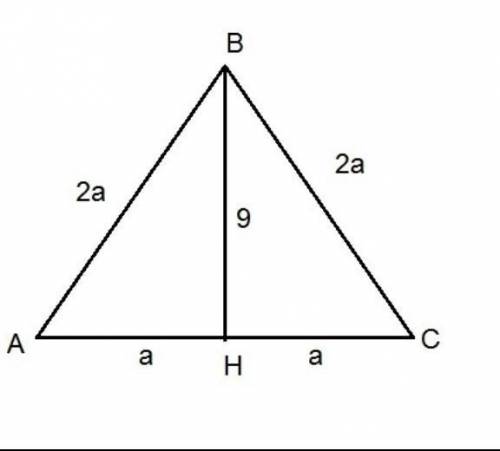
Дано:
ΔАВС - равносторонний
ВН=9 см
Найти:
S=? см²
Решение
Площадь треугольника равна:
S=1/2×АС×ВН, где
АС - длина основания, АС=АВ=ВС (у равностороннего треугольника)
ВН - высота
Пусть АС=2а см, тогда АН=1/2×АС=1/2×2а=а см.
По теореме Пифагора:
АВ²=ВН²+АН²
(2а)²=9²+а²
4а²-а²=81
3а²=81
а²=81÷3
а²=27
а=√27=√9×3=3√3 см
Площадь равна:
S=1/2×9×3√3=1/2×27/√3=27√3/2=13,5√3 см²
ОТВЕТ: площадь равна 13,5√3 см²
Объяснение: