задача2.
1)для начала надо найти радиус R.
для его нахождения следует использовать формулу Пифагора.
L^2=R^2+H^2.
R=под корнем L^2-H^2=под корнем 4^2-2^2=2 корней из 3.
2)далее по формуле нахождения площади поверхности конуса.находим
S=пи*R*L.
S=3,14*2 корней из 3*4=25,12 корней из 3.
задача3.
1)запишем формулу объема шара.
V=4/3*пи*R^3.
R1+R2+R3=V.
12=4/3*3,14*R^3.
4=12,56*R^3.
R=3 под корнем(0,318)
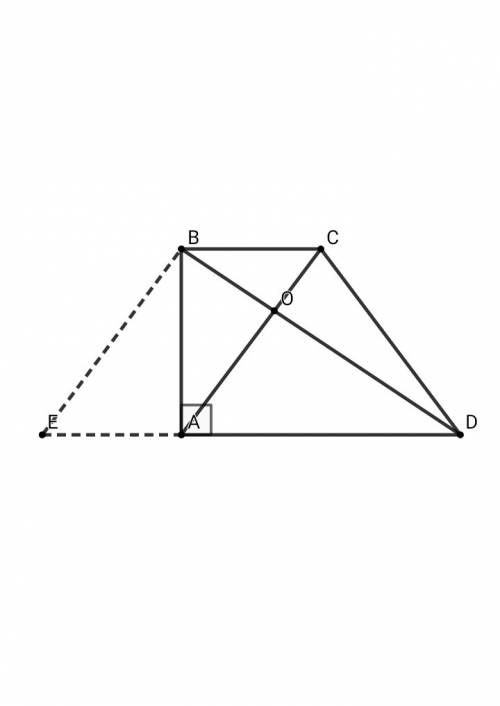

Объем пирамиды = V = S осн · H / 3
1) найдем H: так как sina = противолежащий катет / на гипотенузу
находим H = sina·L.
2) найти R описанной окружности основания..т.е 2h/3..R= cosa·L=2h/3 = h = (3 cos a · L)/2..
треугольника..a(квадрат)а(квадрат)/4 = h(квадрат)..a = (3 cos a ·L) / корень из 3...подставляем под формулу для вычисления площади треугольника = a ((квадрат) корень из 3 )/4 ..получаем S = 3 cos(квадрат) A · L(квадрат) · корень из 3 / и все деленное 4..теперь все подставляем в формулу V для объема..
V = 3 · Cos(квадрат) А · sin A · L (куб)· корень из 3 и все деленное на 4
1. объем куба равный объему параллелепипеда
V=15·50·36=27000см³
Ребро куба ∛27000=30 см
2. Радиус основания конуса
r=√4²-2²=√12=2√3 м
Площадь боковой поверхности круглого конуса равна произведению половины окружности основания (C) на образующую (l):
S=½ C l=π r l
S=½ C l=π 2√3 ·4=8√3π м²
3.Формула объема шара V=4/3 π R³
Для того, чтобы узнать радиус шара объема, равного сумме объемов этих трех шаров, найдем объем каждого из них:
V₁=4/3 π 27=36π
V₂=4/3 π 64=85 ⅓π
V₃=4/3 π 125=166 ⅔π
Общий объем шаров:
V=36π+85 1/3π+166 2/3π=288π см³
288π=4/3 π R³
R³=288π*3:4π=216см³
R=∛216=6 см