9.03.2020 Задания по суммативному оцениванию за 3 четверть
Суммативное оценивание за раздел «Решение треугольников»
Тема
Решение треугольников
Задання
Вариант-1
1. В треугольнике известны две стороны b=10см, с=4см и угол между ними а=60°.
Найдите третью сторону треугольника.
2. В треугольнике ABC AB=3см, LB=40°, LC=70°. Найдите сторону AC.
3. Дан треугольник ABC, как показано на рисунке. Найдите радиус описанной
окружности, если ВД=12см, АД=5см. ДС-9см.
В B.
A
С

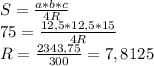
В треугольнике, образованном высотой, проведенной к основанию, боковой стороной и половиной основания (данный нам треугольник равнобедренный) биссектриса угла при основании делит эту высоту в отношении 5:4, значит по свойству биссектрисы: "Биссектриса делит сторону, противолежащую углу в отношении сторон, образующих данный угол", имеем: (Х-9)/(Х/2)=5/4 или (9-Х)*2/Х=5/4. Тогда 8Х-72=5Х, отсюда Х=24. Итак, по Пифагору искомая высота равна
√[(Х-9)²-(X/2)²]=√(15²-12²)=9см.
ответ: высота, проведенная к основанию, равна 9см.