1) Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.
2) Все 3 признака равенства треугольников:
а) Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
б) Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
в) Если 3 стороны одного треугольника соответственно равны 3-ем сторонам другого треугольника, то такие треугольники равны.
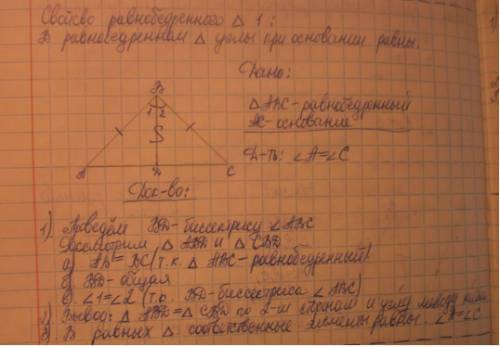
3) Треугольника называется равнобедренным, если 2 его стороны равны.
В равнобедренном треугольнике углы при основании равны.
4) Отрезок угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны называется биссектрисой треугольника. Биссектриса делит угол на 2 равные части.
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны называется медианой треугольника.
Перпендикуляр, проведенный из вершины треугольника к прямой, соединяющей противоположную сторону, называется высотой треугольника.
--------
Чертежи во вложениях



Так как ABCD - параллелограмм, AB параллельна CD, значит угол AKD =CDK , как накрест лежащие углы при параллельных прямых AB и CD, с секущей KD.
угол AKD=ADK, AKD=CDK, следовательно угол ADK = CDK, следовательно DK -биссектриса, чтд.
ABCD - параллелограмм, следовательно AB=BC.
Из доказанного - AD=AK
AD=BC, AD=AK, следовательно AD=AK=BC=4
AB=AK+KB=4+3=7
AB=CD=7, т к ABCD -параллелограмм
P=(4+7)*2=11*2=22