Боковое ребро наклонной призмы равно 14 см и составляет с плоскостью основания угол 30º. Нужно найти высоту призмы.
-------------
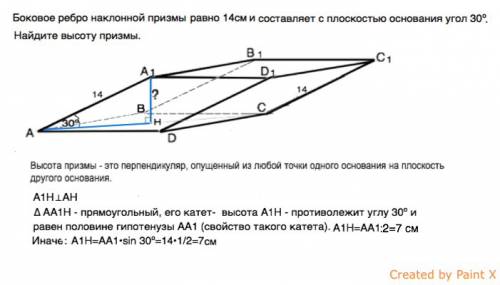
Высота призмы - это перпендикуляр, опущенный из любой точки одного основания на плоскость другого основания.
Т.к. основания лежат в параллельных плоскостях, высота призмы равна расстоянию между плоскостями, содержащими её основания.
Обозначим вершины призмы ABCDA1B1C1D1 (см.рисунок в приложении)
Опустим из вершины А1 перпендикуляр А1Н на плоскость основания.
А1Н ⊥АН
∆ АА1Н - прямоугольный, его катет- высота призмы А1Н - противолежит углу 30º и равен половине гипотенузы АА1.
А1Н=14:2=7 см
Иначе: А1Н=АА1•sin 30º=14•1/2=7см
–––––––––
Примечание:
Высота призмы не обязательно совпадает с высотой боковой грани. Она совпадает с ней, только если призма прямая. В данном случае призма - наклонная.
Чуть позже объясню почему. (рисунок 1)
Соединим середины сторон 4 угольника ABCD.
Проведем диагональ AC
Очевидно что MN-средняя линия треугольника ABC,откуда
MN||AC, также PQ-cредняя линия треугольника ACD ,то PQ||AC.
То выходит что MN||PQ. Анологично при проведении другой диагонали докажем что MQ||NP. То MNPQ-параллелограмм.
Рассмотрим наконец 6 угольник проведем в нем диагональ D (2 рисунок)
Она бьет его на 2 четырехугольника.
На ней отметим точку S,являющуюся серединой диагонали.
То из выше сказанного A1A2A3S-параллелограмм.
Понятно , что для точек A1 A2 A3 cуществует одна и только одна точка
H, для которой A1A2A3H-параллелограмм. А значит точка H совпадает с точкой S. H=S Тк второй такой точки не существует.
Рассуждая анологично для второго 4 угольника. Покажем что
M=S.
А значит формально говоря: H=M
ЧТД.