ответ: РМ=√3
Объяснение:
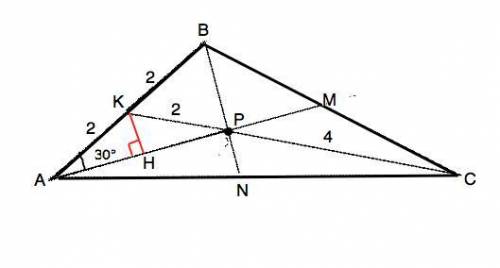
Медианы треугольника пересекаются в одной точке. Следовательно, отрезок СР - часть медианы из С, Продолжим ее до пересечения с АВ в точке К.
Медианы треугольника точкой пересечения делятся в отношении 2:1, считая от вершины. ⇒ РК=СР:2=4:2=2.
Точка К - середина АВ. ⇒
АК=КВ=2.
Треугольник АКР равнобедренный ( АК=КР).
Из К опустим высоту КН на АР. Отрезок КН=АК:2=1 (свойство катета, противолежащего углу 30°).
Тогда АН=НР=КН•ctg30°=√3 ⇒ АР=2√3
По свойству медиан АР:РМ=2:1, поэтому РМ=0.5•2√3=√3
Дано:АВС-треугольник,<А =100°,<С : <В=2:3
Найти:<В,<С.
<А+< В+ <С= 180°
<В +<С= 180°-<А= 180°-100°=80°
<С : <В = 2:3
2+3=5 - частей
80° ÷ 5= 16°- в одной части
<С= 2•16°=32°
<В= 3•16°= 48°
ИЛИ:
<А+< В+ <С= 180°
<В +<С= 180°- <А= 180°-100°=80°
<С : <В = 2:3
пусть х- количество °(градусов) в одной части:
2х+3х=80°
5х=80°
х=16°
<С=2х=2•16°=32°
<В=3х=3•16°=48°