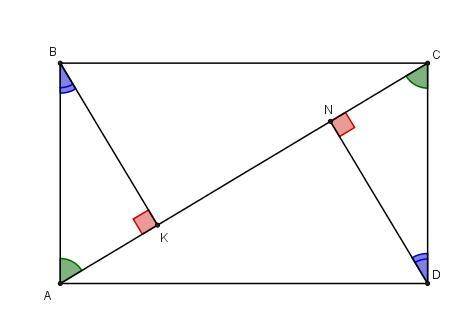
∠BAC = ∠ACD как накрест лежащие углы при AB || CD и секущей AC.
AB = CD, следовательно, ΔABK = ΔCND по гипотенузе и острому углу
У равных треугольников соответствующие элементы (стороны, углы) равны, т.е. BK = DN; CN = AK.
Рассмотрим прямоугольный треугольник BKC: по т. Пифагора
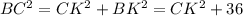 (*)
(*)
Рассмотрим прямоугольный треугольник ABC: по т. Пифагора
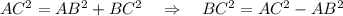
Подставляем теперь в равенство (*), получаем
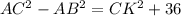
AB² найдем по теореме Пифагора из прямоугольного треугольника ABK, значит
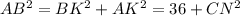
Все данные у нас есть, осталось решить уравнение
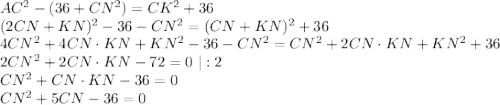
Получили квадратное уравнение, которое можно решить через дискриминант
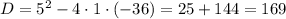
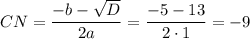 - не удовлетворяет условию
- не удовлетворяет условию
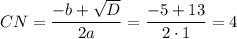 см
см
Следовательно, AC = 2*4 + 5 = 13 см, тогда
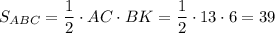 см²
см²
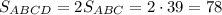 см²
см²
Второй решения:
У треугольников ABK и BKC прямые углы равны и ∠ABK = ∠BCK, следовательно, ΔABK ~ ΔBKC, из подобия треугольников следует, что BK/CK = AK/BK
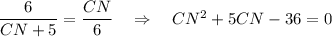
Такое же уравнение как в первом
ответ: 78 см².
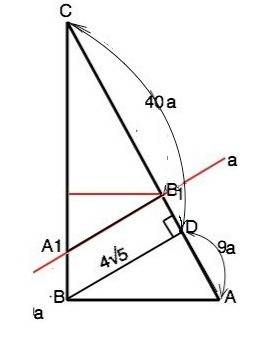
Пусть прямая а пересекает АС в т.В1, ВС в т.А1.
А1В1 делит ∆ АВС на две равновеликие части, т. е. на треугольник и четырехугольник равной площади.
S ∆ А1B1C=S BАB1А1= S ∆ABC:2
Прямоугольные треугольники с общим острым углом подобны.
∆ CA1B1~ ∆ СAB.
Площади подобных фигур относятся как квадраты отношения линейных размеров их сходственных элементов.
k²=2 ⇒ k=√2
АВ:А1В1=√2 ⇒ A1B1=AB:√2
АВ найдем из ∆ АВD.
Примем коэффициент отношения отрезков AD:CD равным х.
Высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу.
Т.е. ВD² =АD•CD
Тогда 80=40•9x²
9х²=2⇒ х=(√2)/3 и AD=9•(√2)/3 =3√2
Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.
АВ²= BD²+AD²
АВ=√(80+9•2)=√49•2=7√2 ⇒ A1B1=7√2:√2=7
ответ: 3 см