Более короткий вариант решения этой задачи ( без решения квадратного уравнения)
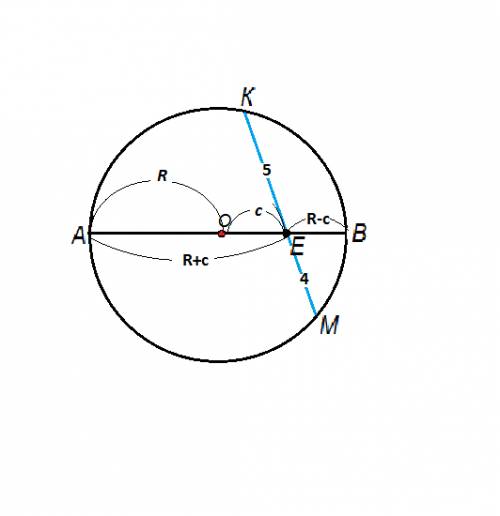
Пусть расстояние от центра О окружности до точки Е на хорде ( не до хорды, а именно до точки) равно с.
Тогда АЕ=6+с, ВЕ=6-с
(6+с)(6-с)=20
Применив формулу сокращенного умножения получим:
36-с²=20
с²=16
с=4
ВЕ=6-4=2 см
АЕ=12-2=10 см
Построение сводится к проведению перпендикуляра из точки к прямой.
Из вершины А, как из центра, раствором циркуля, равным АС, делаем насечку на стороне ВС. Обозначим эту точку К.
∆ КАС- равнобедренный с равными сторонами АК=АС.
Разделив КС пополам, получим точку М, в которой медиана ∆ КАС пересекается с основанием КС. Т.к. в равнобедренном треугольнике медиана=биссектриса=высота, отрезок АМ будет искомой высотой.
Для этого из точек К и С, как из центра, одним и тем же раствором циркуля ( больше половины КС) проведем две полуокружности. Соединим точки их пересечения с А.
Отрезок АМ разделил КС пополам и является искомой высотой ∆ АВС из вершины угла А.
непонятное можешь спросить