5,5
Погоджуюсь з першою відповіддю
(см. объяснение)
Объяснение:
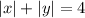
Перед нами уравнение квадрата, точка пересечения диагоналей которого имеет координаты (0; 0) и расстояние от точки пересечения диагоналей которого до одной из вершин равно 4.
Зная это, построим график:
(см. прикрепленный файл)
Задание выполнено!
Комментарий 1:
Функция непрерывна и при любом раскрытии модуля будет получаться уравнение прямой: либо y=-x+4, либо y=-x-4, либо y=x-4, либо y=x+4. Строим их до пересечения, таким образом получая график.
Комментарий 2:
Функция непрерывна и при любом раскрытии модуля будет получаться уравнение прямой, причем точки "склеивания" будут в координатах (0; 4), (4; 0), (-4; 0), (0; -4). Тогда соединим их и получим график.
Комментарий 3:
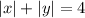
При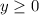 
получим график модуля 
.
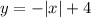При 
будет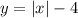 
.
Строим это и получаем график.
AC:16=7:3––АС=16•7:3=28 см
Объяснение:
Примем коэффициент отношения отрезков на АВ равным а,Так как AM : MB = 3:4, то АВ=АМ+ВМ=7а ⇒ AM:AB = 3:7.
CN:CB = 3:7- дано.
а) Точки М и N лежат в плоскости ∆ АВС и в плоскости α. ⇒MN - линия пересечения этих плоскостей.
МN и АС высекают на прямых АВ и ВС пропорциональные отрезки.
Из обобщённой теоремы Фалеса: если отрезки, высекаемые прямыми на одной прямой, пропорциональны отрезкам, высекаемым теми же прямыми на другой прямой, то эти прямые параллельны.⇒ АС║MN.
Если прямая (АС), не лежащая в плоскости α, параллельна некоторой прямой (MN), которая лежит в плоскости α, то прямая параллельна плоскости . ⇒АС || α
б) Т.к. MN║AC, углы при их пересечении секущими АВ с одной стороны и ВС с другой равны как соответственные. Отсюда следует подобие треугольников MBN и ABC с коэффициентом подобия k=BC:NC=7:3 ⇒ AC:MN=7:3
AC:16=7:3––АС=16•7:3=28 см
5,5 наверное