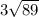
Объяснение:
Объём пирамиды:
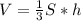, где S - площадь основания, h - высота пирамиды.
Значит 
У правильной четырёхугольной пирамиды основанием выступает квадрат. Если сторону квадрата обозначить как а, то S=a² ⇒ а=√S.
Боковое ребро пирамиды l, её высота h и полудиагональ основания образуют прямоугольный треугольник, в котором искомое ребро - гипотенуза, а высота и полудиагональ - катеты.
Диагональ квадрата равна √(2а²)=а*√2,
тогда половина диагонали равна а/√2, а так как а=√S,
то половина диагонали равна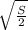 
Тогда, по теореме Пифагора:
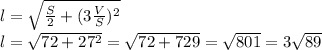
ответ: ВД приблизительно 73,32см
Объяснение: так как нам известно, что сторону АД =80 ° делит высота ВН, отсекая от неё отрезок 32см, то второй отрезок будет: 80-32=48см;
АН=32см; НД=48см. Рассмотрим ∆АВН- он прямоугольный и ,зная в нём две стороны, найдём по теореме Пифагора высоту ВН:
ВН²=64²-32²=4096-1034=3072=√3072
ВН=√3072см. Теперь рассмотрим ∆ВДН - он тоже прямоугольный и, зная высоту ВН мы можем найти диагональ ВД- расстояние между вершинами тупых углов по теореме Пифагора:
ВД²=48²+3072= 2304 +3072=5376
ВД=√5376=√256×√21=16√21(см). Если округлить до сотых будет приблизительно 73,32(см)