
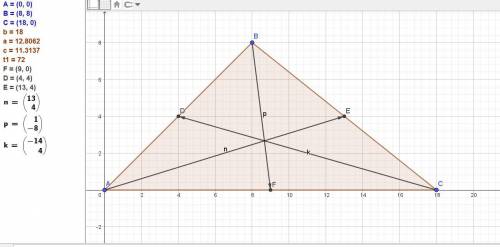
Дан треугольник АВС, угол А = 45 градусов, АВ =8 √2 и АС = 18.
Поместим его в прямоугольную систему координат точкой А в начало, точка В на оси Ох.
х(В) = AB*cos A = 8√2*(√2/2) = 8.
y(B) = AB*sin A = 8√2*(√2/2) = 8.
Получили координаты вершин.
А(0; 0), В(8; 8), С(18; 0).
Находим векторы сторон.
Координаты векторов
АВ ВС АС
х у х у х у
8 8 10 -8 18 0.
По свойству векторов медиана как половина диагонали параллелограмма на векторах сторон равна половине суммы векторов сторон.
Медианы
АА1 ВВ1 СС1
х у х у х у
13 4 1 -8 -14 4.
Модули (длины) медиан равны:
|AA1| = √(13² + 4²) = √(169 + 16) = √185 ≈ 13,60147.
|BB1| = √(1² + (-8)²) = √(1 + 64) = √65 ≈ 8,06226.
|CC1| = √((-14)² + 4²) = √(196 + 16) = √212 ≈ 14,56022.
S осн = 6*а^2*корень из 3/4.
Видим, что надо знать сторону основания :а-?
3)S бок = 6*0,5* а*h, где h- апофема .Таким образом, от цели нас отделяет только нахождение стороны основания а. Из тр-ка МОS-прям.: SO = 12, SM =15, тогда ОМ=9 ( либо по теореме Пифагора, либо этот тр-к подобен "египетскому" с коэфф 3).
4)Из тр-ка АОМ-прям: ОМ =9 ,угол ОАМ =60 град., тогда АМ =9/корень из 3 = 3*корень из 3, тогда а = 2*АМ = 6*корень из 3.
5)Sполн = 6* (6*корень из 3)^2 *корень из 3/4+ 3* 6*корень из 3*15 =
= 6*36*3* *корень из 3/4 + 18*15* корень из 3= 6*9*3* *корень из 3 + 18*15* корень из 3 = 18*24* корень из 3 = 432* корень из 3 (кв.ед).