В задачах на построение используются только такие инструменты: циркуль и линейка.
По условию задачи у нас есть отрезок и угол. А так как у равнобедренного треугольника углы при основании равны, то нам нужно построить треугольник по стороне и двум прилежащим к ней углам - это одна из основных задач на построение (см. учебник по геометрии за 7 класс).
Построение.
1. Проводим прямую.
2. На прямой берем точку А и откладываем отрезок, равный данному (с циркуля, еще одна основная задача на построение). Получаем точку С.
3. От точки А откладываем угол, равный данному (с циркуля, еще одна основная задача на построение).
См. приложение
4. От точки С откладываем угол, равный данному (аналогично п. 3).
5. Стороны углов пересекутся в вершине В треугольника .
Искомый равнобедренный треугольник построен.
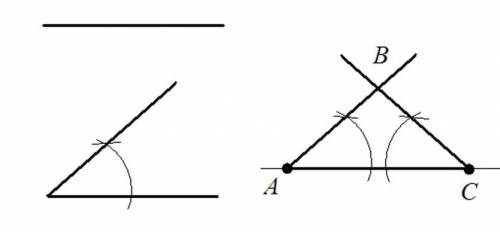
Искомая площадь равна половине произведения высоты пирамиды на основание треугольника со сторонами апофема, ребро, и основанием - высота треугольника в основании.
Половину стороны основания найдем по теореме Пифагора.
х= √(11²-7²)=√121-49=6√2
Cторона основания равна
2*6√2=12√2
Высота правильного треугольника h равна
h=а√3:2=12√2*√3:2=6√6
Основание высоты пирамиды находится на расстоянии 1/3 от основания апофемы, так как центр ее - на пересечении медиан ( они пересекаются в отношении 2:1 от вершины) и это расстояние равно 2√6
Найдем высоту пирамиды.
h=√49-24=√25=5
Площадь сечения
S=(5*6√6):2=15√6 см²