ответ: 54 см
Объяснение:
Проведем прямую ВК, параллельную диагонали АС, К - точка пересечения этой прямой с прямой AD.
ВК ║АС, AD ║ ВС, значит КВСА - параллелограмм, ⇒
АК = ВС = 5 см,
ВК = АС = 9 см.
Если ВН высота трапеции, то
Sabcd = 1/2 (AD + BC) · BH
Рассмотрим ΔКВD:
KB = 9 см, BD = 12 см, KD = КА + AD = 5 + 10 = 15 см, ВН является высотой треугольника.
Skbd = 1/2 KD · BH = 1/2 (KA + AD) · BH = 1/2 (BC + AD) · BH
Сравнивая формулу площади трапеции и площади треугольника видим, что
Sabcd = Skbd.
Найдем площадь треугольника KBD по формуле Герона.
p = (KB + BD + KD)/2 = (9 + 12 + 15)/2 = 18
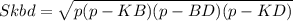
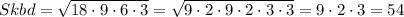 см²
см²
Sabcd = 54 см²

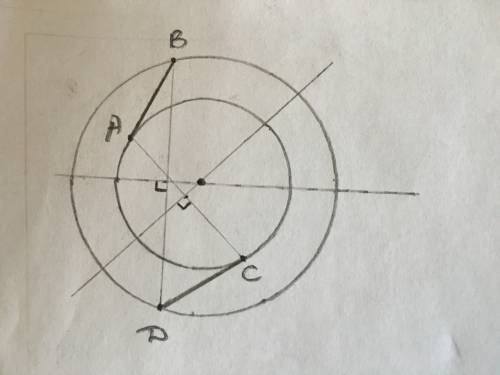
Треугольники AOD и BOC подобны по свойству трапеции.
Площади подобных треугольников относятся, как квадраты коэффициента их подобия
25:16=k²
k=√(25:16)=5:4
Следовательно, основания трапеции относятся, как 5:4
Обозначим
высоту ᐃ ВОС=h₁
высоту ᐃ АОD=h₂
S АОD=h₂·АD:2
S ВОС=h₁·ВС:2
Площадь трапеции равна произведению ее высоты на полусумму оснований:
Высота трапеции Н
S ABCD=Н·(АD+ВС):2
Н=h₂+h₁
S ABCD =(h₁+h₂)·(АD+ВС):2=
=h₁·АD+h₂·АD+h1·ВС+h₂·ВС
1)
Применим свойство пропорции: произведение средних членов пропорции равно произведению крайних.
h₂:h₁=5:4
4h₂=5h₁
h₂=5h₁/4
S AOD=h₂·АD:2=5h₁/4·АD:2
25=5h₁/4·АD:2 Умножим на два обе части уравнения
12,5=5h₁/4·АD
5h₁/4 =12,5:AD
h₁:4=2,5:AD
h₁·AD= 4·2,5 =10 см²
Т.к. площади боковых треугольников у трапеции равны равны, то h₂·ВС=10 см²
Проверим это:
2)
h₂:h₁=5:4
5h₁=4h₂
h₁=4h₂/5
S ВОС=h₁·ВС:2=4h₂/5·ВС:2
16=4h₂/5·ВС:2 Умножим на два обе части уравнения
8=4h₂/5·ВС
4h₂:5=8:ВС
4h₂·ВС=8·5=40
h₂·ВС=40:4=10 см²
3) Подставим значения h₂·ВС и h₁·AD в уравнение площади трапеции
S ABCD=h₁·АD+25+16+h₂ВС=41+=h₁·АD+h₂·ВС =
S ABCD=10+25+16+10= 61 см
Объяснение:
S ABCD=10+25+16+10= 61 см