Пусть дан равнобедренный треугольник АВС, у которого АС=12 см - основание, АВ=ВС=18 см - боковые стороны. Отложим отрезки BE=BF=х соответственно на боковых сторонах треугольника АВ и ВС. Тогда АЕ=CF=18-x. Т. к. Образовалась равнобокая трапеция AEFC, то АСIIEF
Треугольник BEF подобен треугольнику BAC, то
BE/BA=EF/AC
x/18=EF/12
EF=12x/18=2x/3
Зная, что периметр трапеции AEFC= 40 см, составим и решим уравнение
2(18-х)+12+2x/3=40
6(18-x)+36+2x=120
108-6x+36+2x=120
4x=24
x=6
Значит BE=BF=6
Доказано, отметьте ответ как лучший
Объяснение:
1. <A = <C = 70° ( внутренние противолежащие углы в параллелограмме равны )
AB = CD, AD = BC, <A = <C
∆ABD = ∆BCD ( по свойству СУС, сторона угол сторона)
2. а) <CAD = <CAB, AD = AB, AC - общая сторона
∆ADC = ∆ABC (СУС)
б) BC = DC (из предыдущего доказательства)
тогда ∆CBD - равнобедренный, тогда CF - высота, биссектриса и медиана (свойство равнобедренного треугольника)
тогда <FCB = <FCD
FC - общая сторона
∆BFC = ∆DFC (СУС)
3. AB = BC (по условию)
тогда ∆ABC - равнобедренный, и BO - биссектриса
=> <ABO = <CBO
BO - общая сторона
=> ∆ABO = ∆CBO
тогда AO = CO
а угол AOE = углу COE = 90°
сторона OE - общая
тогда ∆AOE = ∆COE (сторона угол сторона)
надеюсь и заслуживаю лайк
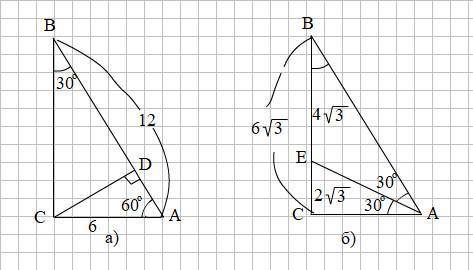
Смотри рисунок на прикреплённом фото.
1) ΔАСD ~ ΔABС по 1-му признаку подобия прямоугольных треугольников: если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то такие треугольники подобны. А у ΔАСD и ΔABС общий острый угол А.
2) Катет АС прямоугольного ΔАВС лежит против угла ∠В = 30°, значит АС равен половине гипотенузы АВ: АС = 0,5АВ = 0,5·12 = 6 (см).
Найдём коэффициент подобия ΔАСD и ΔABС по отношению их гипотенуз АС : АВ = 6/12 = 1/2. Следовательно, коэффициент подобия этих треугольников k = 1/2. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
S(ΔACD) : S(ΔABC) = k² = 1 : 4.
3) Найдём величину катета ВС, используя теорему Пифагора:
ВС = √(АВ² - АС²) = √(12² - 6²) = √108 = 6√3 (см)
Известно, что биссектриса угла делит противолежащую сторону на отрезки, пропорциональные прилежащим к углу сторонам. Поэтому СЕ : ВЕ = АС : АВ = 1/2.
Тогда СЕ = 1/3 · ВС = 2√3 (см) и ВЕ = 2/3 · ВС = 4√3 (см)
Смешное решение, если не понравится - можете банить.
Ясно, что отрезки по обеим боковым сторонам равны.
Если длина этих отрезков 0, то периметр совпадает с периметром треугольника и равен 48. Если длина отрезков 18, то периметр трапеции будет равен 2 основаниям, то есть 24 (это такая совсем "вырожденная" трапеция с боковыми сторонами, равными 0).
Если обозначить длину отрезков за x, а периметр трапеции y, то все строны трапеции зависят от x линейно - боковые стороны равны 18 - x, малое основание просто пропорционально x (я намеренно не считаю, как именно пропорционально), поэтому графиком зависимости y(x) будет прямая линия, проходящая через точки (0,48) и (18,24);
уравнение такой прямой записать просто -
(y - 48)/(x - 0) = (24 - 48)/(18 - 0);
y = - x*4/3 + 48;
или, что - то же самое, x = 3/4*(48 - y);
При y = 40; x = 6; :
Вся соль - в прямой линии. :)