У цилиндра и конуса одно основание. Радиус основания R=d/2 = 8/2=4 дм
Образующая по теореме Пифагора L = √4²+3²=√25= 5 дм
Объем цилиндра V = πR²h = 16*3π = 48π дм³
Объем конуса V = πR²h/3 = π*16*3/3 = 16π дм³
Напишу для первого
За т.синусов
MN MK
=
sinK sinN
Найдем кут K
КутК=180-(КутN+КутМ)
180-(20+80)=80
sinK = 0.984
sinN = 0.984
MN = (МК x sinK):sinN
MN = (10 x 0.984):0.984 = 10
И тут я понял, что скорее всего вам нужно найти сторону MN через равнобедренность треугольника (скорее всего тему косинусов вы еще не проходили), поэтому напишу второе решение:
Докажем равнобедренность треугольника
КутК=180-(КутN+КутМ)
180-(20+80)=80
Так как углу углы при основе одинаковые, то треугольник равнобедренный и из этого выплывает что МК=MN=10
У параллелограмма всего 4 угла. В параллелограмме есть пара острых равных между собой углов, а также пара равных тупых углов (случай прямоугольника опустим, у него все углы равны, в этой задаче такого нет). Поэтому если мы найдем острый угол, а также тупой угол параллелограмма, то мы нашли все углы.
Теперь найдем их Ситуация следующая: есть две параллельные прямые, каждая из смежных с ними сторон является секущей. Получается, что имеются две пары односторонних друг для друга углов. Рассмотрим любую из них (для второй все то же самое)
Пусть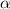 
- острый угол, 
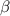- тупой. Тогда имеет место соотношение
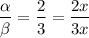
Известно, что сумма односторонних углов равна 180°, получаем вот такое уравнение:
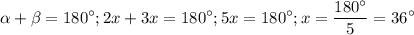
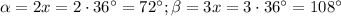
ответ: 72°, 72°, 108°, 108°
Использован египетский треугольник, формулы объема конуса и цилиндра