1.Теорема пифагора. sqrt(5^2+12^2)=sqrt(169)=13
2.теорема пифагора sqrt(289-225)=8
3.Диагонали в точке пересечения делятся пополам.
Теорема пифагора sqrt(36+64)=10
4.Аналогично третьему 12.
5.второй угол=30(90-150=30)
высота = 6(катет напротив 30 равен половине гипотенузы
S=16*6=96
6.В равнобедренном высота также медиана => основание=2*sqrt(169-25)=24
S=24*5/2=60
7. h=sqrt(169-25)=12
S=(10+20)*12/2=180
8.CH=CD=10(Углы C и D =45)
AH=18-10=8 =>BC=8
S=(18+8)*10/2=130
Прости, что кратко, уж очень много писать
1)гипотенуза=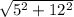
=13см ( по т. Пифагора)
2)катет=
=8 см
3)В ромбе диагонали точкой пересечения делятся пополам и пересекаются под прямым углом, следовательно получаем
1катет=6 см, 2катет=8 см
сторона=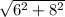
=10cм
4)Т.е. нужно найти катет из треуг. с гипотенузой 10 см и катетом 16:2=8см
2 катет=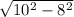
=6cм
ТОгда диагональ = 6*2=12см
5)S=a*b*sin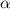
S=16*12*0,5=96cм^2
6)1/2 основания =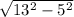 
=12cМ
Основание треуг.=12*2=24см
S=0,5*24*5=60cм^2
7) Высота=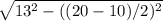
=12см
S=a*ah=20*12=240cм^2
8)Высота СН=АВ=10см
треуг. DНС-р/б
НD=HC=10cМ
ВС=18-10=8см
S=(18+8)/2*10=130см^2
1. ВС - малое основание. Тр-ки ВОС и DOE подобны, ВС/ВО = DE/DO; ВС = 12*3/9 = 4
2. ВР - биссектриса, угол АВР = угол СВР, но угол СВР = угол ВРА => тр-к АВР равнобедренный, АВ = ВР = 10; аналогично DP = CD = 10; AD = 20;
периметр (10 + 20)*2 = 60; (интересно в этой простенькой задачке то, что сторону вычислить можно, а углы - нет: подходит любой параллелограмм, у которого одна сторона в 2 раза больше другой).
3. Пусть равнобедренная трапеция АВСЕ, АЕ II ВС; ВН - высота,
ВЕ = √65; BH = 4; HE = √(65 - 16) = √49 = 7;
При этом ЕА = (АЕ - ВС)/2; поэтому НЕ = АЕ - (АЕ -ВС)/2 = (АЕ + ВС)/2;
S = BH*(АЕ + ВС)/2 = 4*7 = 28;