
ответ: 9√3 см³
Объяснение:
Если боковые ребра пирамиды равны, то высота проецируется в центр окружности, описанной около основания. В прямоугольнике - это точка пересечения диагоналей.
Итак, SO - высота пирамиды, тогда ОА - проекция бокового ребра SA на плоскость основания, следовательно ∠SAO = 45° - угол наклона бокового ребра к плоскости основания.
ΔSOA прямоугольный, острый угол равен 45°, значит он равнобедренный.
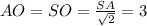 см (так как гипотенуза равнобедренного прямоугольного треугольника с катетом а равна а√2 )
см (так как гипотенуза равнобедренного прямоугольного треугольника с катетом а равна а√2 )
Диагонали прямоугольника равны и точкой пересечения делятся пополам:
BD = АС = 2АО = 6 см
Sabcd = 1/2 AC · BD · sin∠AOD
Sabcd = 1/2 · 6 · 6 · √3/2 = 9√3 см²
V = 1/3 Sabcd · SO = 1/3 · 9√3 · 3 = 9√3 см³
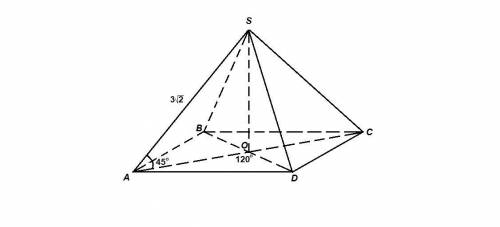
Пусть <C1BA1=α. В прямоугольном треугольнике ВС1С угол ВСС1
равен 90-α. Но <C1MA1 - центральный и равен 2<BCC1, так как <BCC1 вписанный и опирается на ту же дугу, что и центральный. Итак, α=2*(90-α), отсюда α=180-2α и α=60°.
Значит <BCC1 и <BAA1 равны по 30°
В прямоугольных треугольниках ВС1С и ВА1А катеты, лежащие против углов 30°, равны половине гипотенузы.
Значит ВС1=(1/2)*ВС =ВL (так как L - середина ВС), а
ВА1=(1/2)*АВ=ВК (по такой же причине).
ВК+С1К=ВL (1)
BL-A1L=BK. (2)
Подставим (2) в (1):
BL-A1L+С1К=ВL. Или С1К=А1L.
Что и требовалось доказать.