1) 60° и 120°
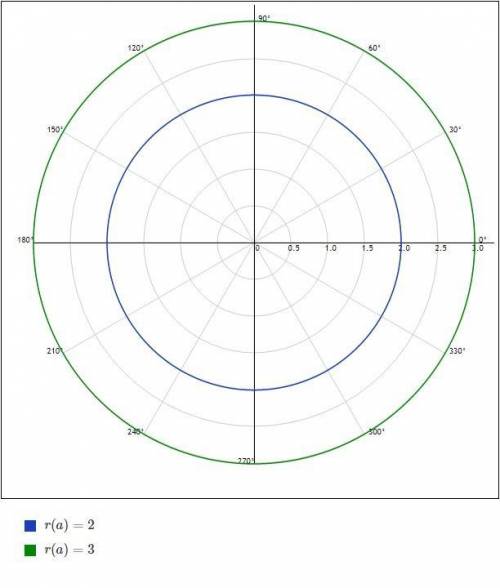
2) в приложении
3) Достаточно двух измерений: любая сторона первого треугольника и любая сторона второго треугольника
Объяснение:
1. Пусть один из углов равен х градусов, тогда второй равен 2х градусов. Сумма двух смежных углов является 180°. Получается уравнение
х+2х=180°
3х=180°
х=180°:3
х=60° - мера меньшего угла
2х=120° - мера большего угла
2. В приложении
3.
Если же в Евклидовой геометрии сравниваем равносторонние треугольники, то достаточно сравнить две любые стороны из каждых сравниваемых треугольников. То есть достаточно сделать два измерения: любая сторона первого треугольника и любая сторона второго треугольника. Если обе эти стороны равны, то треугольники равны. Если же они не равны, то треугольники не равны.
Задание 1:
Смежные углы в сумме равны 180°. Пусть меньший угол равен x, тогда больший 2x. Имеем: x+2x=180 => x=60° -градусная мера меньшего угла. Тогда 120° - градусная мера большего угла.
Задание 2: (см фото, где точка О заменена на точку А - центр окружности)
Задание 3:
По третьему признаку равенства треугольников треугольники равны, если соответственно равны 3 их стороны. В равностороннем треугольнике все стороны равны, а значит, если одна сторона равностороннего треугольника соответственно равна стороне другого равностороннего треугольника, то такие треугольники равны. ответ: 2 измерения - сторону первого треугольника и соответственно сторону второго.
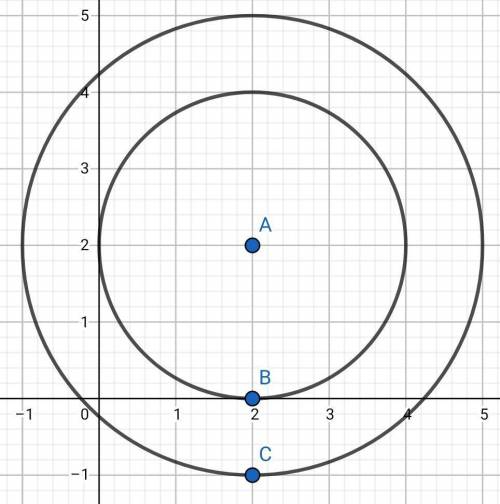
ответ 100% верный))
Соединим поочередно В и А с D.
В ∆ KBD и ∆ KAD ∠KBD =∠KAD – опираются на диаметр ⇒прямые.
Тогда, так как по условию ∠КВО=∠КАО, то ∠ОВD=∠OAD.
Отсюда следует равенство равнобедренных ∆ BOD=∆ AOD с боковыми сторонами-радиусами.
В треугольниках ОВК и ОАК стороны ВО=АО (радиусы), углы при О равны как смежные равным углам ВОD и AOD, следовательно,
∆ ОВК =∆ ОАК по второму признаку равенства треугольников. ⇒ КВ=КА. Доказано.