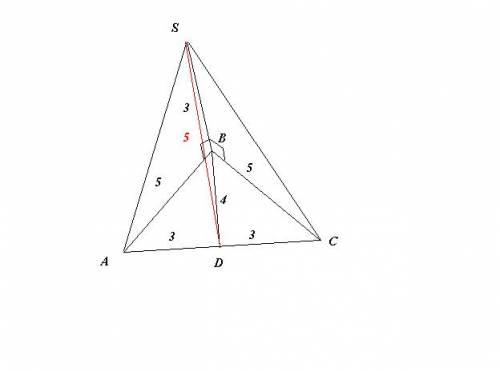
Отрезок BS перпендикулярен плоскости треугольника АВС и имеет длину 3 см. Найдите расстояние от точки S до стороны АС, если АВ = ВС = 5см, АС = 6см
Треугольник АВС равнобедренный его высота ВD=√5²-(6/2)²=√16=4
Расстояние SD определим по теореме Пифагора SD=√3²+4²=√25 = 5 cм
Обозначим параллелограмм буквами ABCD. Пусть диагональ BD образует углы:
угол DBA=30 градусов, угол DB=90 градусов
Обозначим сторону AB=a, сторону BC=b. Так как у параллелограмма противолежащие стороны равны, то AB=CD=a, BC=AD=b
По условию задачи периметр параллелограмма равен:
P=AB+BC+CD+AD=a+b+a+b=2(a+b)=36
a+b=18
Рассмотрим треугольник ABD. Он прямоугольный, угол BDA=90 градусов
Выразим сторону AD:
AD=AB*sinABD=a*sin30=a/2
Значит, b=a/2
Подставим b вместо a:
a+b=36
a+a/2=18
3a/2=18
a=12
b=6
ответ: стороны параллелограмма равны 6см и 12см.
Треугольник АВС - равнобедренный АВ=ВС=5см. Проведем ВК перпендикулярно АС,то ВК - высота, медиана и биссектриса треугольника АВС. АК=СК=3 см. Треугольник АВК - египетский, то ВК=4 см. По теореме о трех перпендикулярах : т. к. ВК перпендикулярно АС, то SK перпендикулярно АС. Значит кратчайшим расстоянием от точки S до стороны АС треугольника АВС является отрезок SK.
Треугольник SBK -египетский, то SK=5 см