Т.к. меньшая боковая сторона прямоугольной трапеции равна 10 см, то ее высота также равна 10 см, а большая боковая сторона :
10:sin 45=10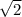
Если в трапецию можно вписать окружность, то сумма оснований равна сумме боковых сторон.
Сумма оснований 10+10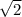
S=(5+5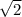 )*10=50+50
)*10=50+50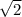
ABC -- нижнее основание, A1B1C1 -- верхнее основание, D -- проекция точки C1 на плоскость основания ABC, C1D -- высота призмы, C1CD=45°
AA1C1C и BB1C1C -- ромбы с острым углом 30°, AA1B1B -- квадрат
Из треугольника C1DC:
sin C1CD = C1D/C1C
sin(45°)=4*корень(2) / C1C
С1С=4*корень(2)/sin(45°)=4*корень(2)/(корень(2)/2)=4*2=8
Так как все боковые грани -- ромбы (квадрат -- это тоже ромб), то длины всех рёбер призмы равны между собой, следовательно, они равны 8.
Площадь боковой поверхности равна сумме площадей ромбов и квадрата.
Sромба=AC*AA1*sin(30°)=8*8*1/2=32
Sквадрата=AB*AA1=8*8=64
Sбок=2*Sромба+Sквадрата=2*32+64=128
найдем вторую боковую сторону 10*sqtrt(2)
если в трапецию можно вписать окружность, суммы длин противоположных сторон
равны. Площадь равна произведению высоты на полусумму оснований.
Сумма оснований по вышесказаному равна половине суммы длинбоковых сторон.
а высота равна меньшей боковой стороне.
S=10(10+10sqrt(2))/2=50(1+sqrt(2))