
2,5
Объяснение:
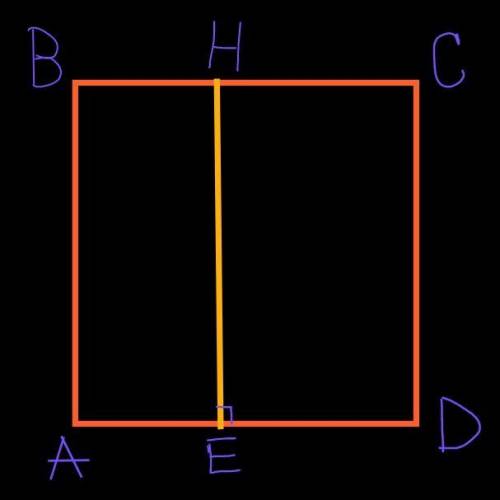
Назовём точки как на рисунке.
Пусть периметр прямоугольника АВНЕ равен 7.
P(прямоугольника)=(а+б)*2,
где а и б стороны прямоугольника. Следовательно а+б=P÷2; тоесть АВ+АЕ=7÷2; АВ+АЕ=3,5
Пусть периметр прямоугольника CDEH равен 8.
P(прямоугольника)=(а+б)*2,
где а и б стороны прямоугольника
Следовательно а+б=P÷2; тоесть CD+DE=8÷2; CD+DE=4.
АЕ+DE=AD. Тогда АВ+АD+CD=3,5+4=7,5.
АВ, AD и CD – стороны квадрата ABCD
Все стороны квадрата равны, следовательно одна сторона равна 7,5÷3=2,5
ответ: 2,5
2,5
Объяснение:
Назовём точки как на рисунке.
Пусть периметр прямоугольника АВНЕ равен 7.
P(прямоугольника)=(а+б)*2,
где а и б стороны прямоугольника. Следовательно а+б=P÷2; тоесть АВ+АЕ=7÷2; АВ+АЕ=3,5
Пусть периметр прямоугольника CDEH равен 8.
P(прямоугольника)=(а+б)*2,
где а и б стороны прямоугольника
Следовательно а+б=P÷2; тоесть CD+DE=8÷2; CD+DE=4.
АЕ+DE=AD. Тогда АВ+АD+CD=3,5+4=7,5.
АВ, AD и CD – стороны квадрата ABCD
Все стороны квадрата равны, следовательно одна сторона равна 7,5÷3=2,5
ответ: 2,5

1.
Не думаю, что в 9 классе проходят ряда Тейлора, наверняка хоть что-то из тригонометрических функций надо было найти по таблице, потому что чаще всего эти функции находят именно по определённым таблицам.
Наверняка ты должен был найти синус по таблице, но почему бы и не найти его другим ?
Так что, вычислим синус с кода(язык — Java), всё очень просто, эта функция из самых лёгких:
//////////////////////////////////////////////////////////////////
public class MyClass {
public static void main(String args[]) {
//угол должен быть в радианах
double radian = 2.6180;
System.out.println(Math.sin(radian));
}
}
///////////////////////////////////////////////////////
Output: 0.5.
Синус равен: 0.5.
А вот зная синус, мы можем простой формулой найти и косинус: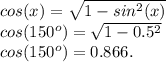
Тангенс найдём по такой формуле:
Вывод: sin = 0.5; cos = 0.866; tg = 0.577.
2.
Зная 2 стороны треугольника, и угол между ними, можем найти третью сторону по теореме косинусов:
Площадь найдём по теореме Герона: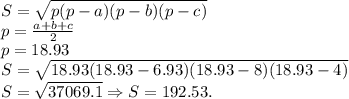
3.
Оставшийся угол равен: 180-(135+30) = 15°
Теперь, зная одну сторону, и углы прилежащие к нему углы, найдём остальные стороны теоремой синусов:
Вывод: b = 10.93.
5.
Для вычисления радиуса вписанной окружности в треугольнике — сначала найдём площадь этого треугольника — по теореме Герона: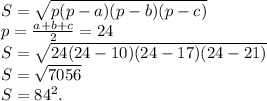
Вывод: r = 3.5.
6.
Зная все стороны, можем найти медианы, медиана, проведённая к стороне 12-и см (b) — равна:
Вывод: медиана, проведённая к самой большой стороне — равна 7 см.