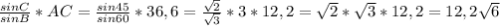звестно, что в выпуклом четырёхугольнике отрезки, соединяющие середины смежных сторон, образуют параллелограмм.
В этом параллелограмме отрезки, соединяющие середины противоположных сторон, являются диагоналями параллелограмма.
По условию эти отрезки (диагонали параллелограмма) перпендикулярны. Следовательно, этот параллелограмм является ромбом.
У ромба все стороны равны. Значит, все отрезки, соединяющие середины смежных сторон, равны.
Отрезок, соединяющий середины двух смежных сторон, параллелелен диагонали и является средней линией треугольника, образованного этими сторонами и диагональю.
Поскольку средние линии всех треугольников равны, то и параллельные им диагонали равны, что и требовалось доказать.
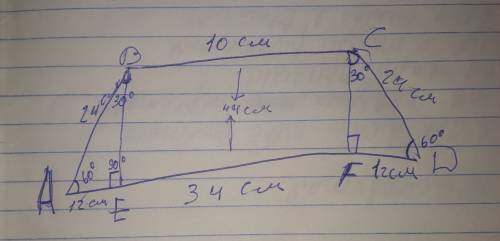
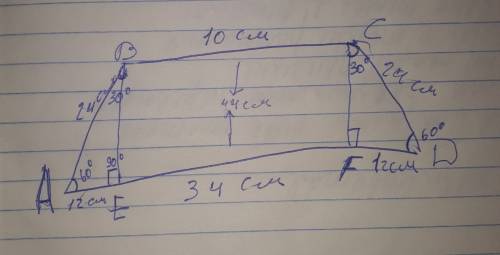
ответ: 12,2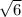
Объяснение:
По теореме синусов
AC/sinB = AB/sinC и отсюда
АВ =