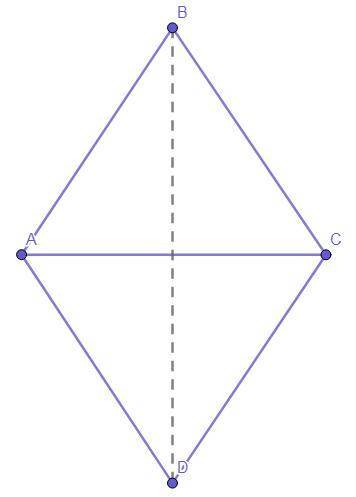
Четырёхугольник ABCD - ромб.
Отрезки АС и BD - диагонали.
АС = АВ.
Найти :Острый угол = ?
Решение :Ромб - это параллелограмм, у которого все стороны равны.
Поэтому -
АВ = ВС = CD = AD.
Рассмотрим ΔАВС.
АС = АВ = ВС.
Следовательно, ΔАВС - равносторонний (по определению равностороннего треугольника).
Каждый угол равностороннего треугольника равен по 60°.Отсюда -
∠ВАС = ∠В = ∠ВСА = 60°.
Диагональ ромба является биссектрисой его угла.То есть -
∠А = 60°*2 = 120°.
Противоположные углы параллелограмма равны.Следовательно -
∠В = ∠D = 60°
∠А = ∠С = 120°.
Отсюда острый угол ромба = 60°.
ответ :60°.
1239,18 см², 3246,62 см².
Объяснение:
Вопрос 1:
Для начала найдём площадь всей фигуры с незакрашенным участком.
Ширина(b) прямоугольника = 32 см.
S=ab.
32×40=1280 см².
Затем найдём площадь всего незакрашенного участка.
S=пR².
4п - площадь меньшего круга. (12,56 см²).
9п - площадь большего круга. (28,26 см²).
12,56+28,26=40,82 см².
1280-40,82=1239,18 см². - S закрашенной фигуры.
Вопрос 2:
a прямоугольника = 60 см.
S прямоугольника = 55×60= 3300 см².
S меньшего круга =3,14 см². Это могло произойти только при том условии, что его R = 1 см.
16×3,14=50,24 см². - S большего круга.
3300-(3,14+50,24)=3246,62 см². - S закрашенной фигуры.
А фото где
Объяснение:
я без фото не могу про мальчика я не знаю потомучто нет фото