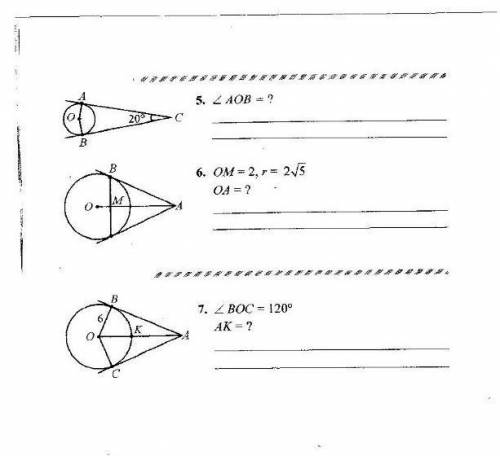
Смотрите на рисунок ...
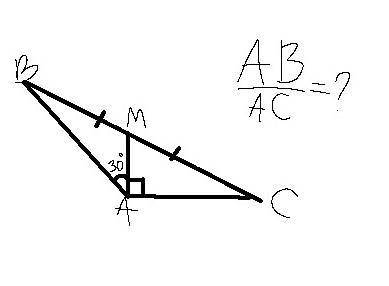
У сторон АВ и АС общая вершина - А, и через неё и проведём медиану АМ к стороне ВС ...
Будем искать:
АС/АВ = ?
ИЛИ
АВ/АС = ?
Итак ...
Что можно сказать про медиану?
Она делит треугольник на два треугольника, площади которых равны ...
Получаем :
1) Площадь треугольника АВМ = площадь треугольника АМС.Рассмотрим треугольник ВМА.
Его площадь можно найти по вот такой формуле:
Площадь треугольника ВМА = ½*АВ*АМ*синус угла ВАМ
По условию угол ВАМ равен 30° ...
Площадь треугольника ВМА = ½*АВ*АМ*синус угла в 30°
Синус в 30° равен ½.
Получаем:
Площадь треугольника ВМА = ¼*АВ*АМ.
Теперь посмотрим на треугольник АМС.
Он прямоугольный... А площадь прямоугольного треугольника равна половине произведения его катетов. (В нашем случае АМ и АС - катеты).
Запишем вот так :
Площадь треугольника АМС = ½*АС*АМ..
ПО ВЫШЕ СКАЗАННОМУ В ПУНКТЕ 1 СЛЕДУЕТ, ЧТО :
½*АВ*АМ = ¼*АМ*АС
½*АВ = ¼*АС
АВ = ½*АС ...
Получаем :
АС/АВ = АС/(½*АС) = 1 : ½ = 2.
АВ/АС = (½*АС)/АС = ½.
(ЕСЛИ НЕВЕРНО ОТМЕТЬТЕ КАК НАРУШЕНИЕ!)
Обозначим вершины призмы А В С Д А1 В1 С1 Д1. В основании правильной четырёхугольной призмы лежит квадрат, по щадь которого вычисляется по формулеS=a², где а- его сторона. Объём призмы вычисляется по формуле:
V=Sосн×h, где h- высота призмы, которой является её боковое ребро.
Sосн=5²=25см²
V=25×1,8=45см³
Площадь полной поверхности призмы - это сумма площадей всех её граней.
Мы нашли площадь основания, так как их 2, то: S2-хосн= 25×2=50см²
Остальные площади найдём по формуле прямоугольника: S=a×b, где а и b - его стороны
Sаа1дд1=1,8×5=9см²;
Так как таких граней 4, то:
S4-хгр=9×4=36см²
Sпол=36+50=86см²
ОТВЕТ: Sпол=86см²; V=45см³