Построено сечение с учётом расположения линий в каждой плоскости.
Длины линий сечения.
AE = √(8² + 4²) = √(64 + 16) = √80 = 4√5.
Длину В1К находим из пропорции (В1К/8 = (8/(8+4)),
отсюда В1К = (8*8)/12 = 16/3.
Тогда ЕК = √(4² + (16/3)²) = √(400/9) = 20/3.
KP = √((8 - (16/3))² + 4²) = √(208/9) = (4/3)√13.
Длину СТ находим из пропорции.
Так как СМ = КС1 = 8 / (16/3) = 8/3, то СМ/СТ = (ВМ/АВ.
Подставим данные. (8/3)/СТ = (8 + (8/3)/8. Получаем СТ = 2.
РТ = √(4² + 2²) = √20 = 2√5.
ДТ = 8 - 2 = 6.
АТ = √(8² + 6²) = 10.
ответ: Р = 4√5 + (20/3) + ((4/3)√13) + (2√5) + 10 =
= 6√5 + (20/3) + ((4/3)√13) + 10.
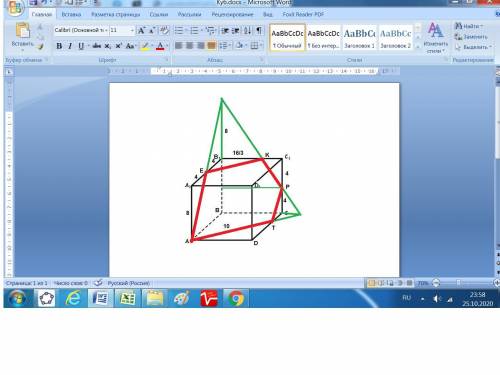
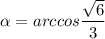
Объяснение:
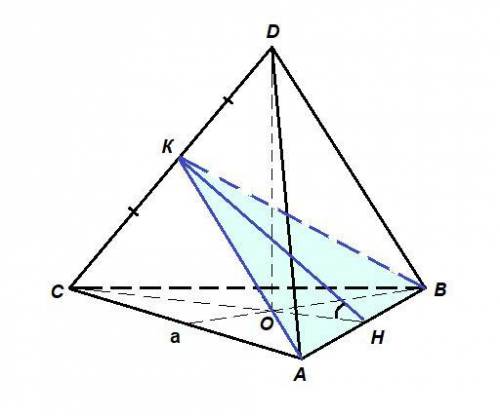
Пусть К -середина CD.
Тетраэдр правильный, все грани - правильные треугольники, тогда АК⊥CD как медиана и высота ΔACD, ВК⊥CD как медиана и высота ΔBCD, значит плоскость (АВК)⊥CD.
АК = КВ (медианы равных равносторонних треугольников)
Пусть Н - середина АВ.
СН⊥АВ как медиана и высота ΔАВС, КН⊥АВ как медиана и высота равнобедренного треугольника АКВ, значит
∠КНС - линейный угол двугранного угла между плоскостями (АКВ) и (АВС) - искомый.
∠KCH = α.
Пусть а - ребро тетраэдра.
 - высоты равных равносторонних треугольников,
- высоты равных равносторонних треугольников,
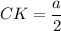
Из прямоугольного треугольника АКН по теореме Пифагора:
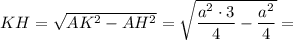
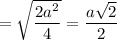
Из ΔКНС по теореме косинусов:
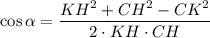
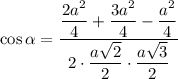

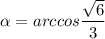
Объяснение:
R=20/2=10(cм)
С=2π×10
С=20π